

České vysoké učení technické
Fakulta stavební
obor geodézie a kartografie
Problematika numerické interpolace drah družic GPS
Místopřísežně prohlašuji, že jsem samostatně vypracoval celou diplomovou práci včetně všech příloh.
V Praze dne 6.12. 2000
Radek Hampl
Poděkování:
V prvé řadě bych velmi rád poděkoval doc. Dr. Ing. Leoši Mervartovi, PhD. za trpělivost, se kterou přistupoval ke konzultacím, které se týkaly řešení některých problémů vzniklých při zpracovávání daného tématu diplomové práce. Další nemalý dík patří Prof. Ing. Janu Kosteleckému, DrSc. za pomoc při otázkách týkajících se použitých časových systémů. A v neposlední řadě pak děkuji doc. Ing. Aleši Čepkovi, CSc. za poskytnuté rady stran programovacího jazyka C++.
Předmluva:
Interpolace drah družic GPS je velmi důležitou součástí určení jejich predikované polohy, to jest souřadnic v geocentrickém
terestrickém souřadném systému. Dnešní metody jsou založeny na složitých modelech drah družic, což je spojeno s velmi složitými
výpočetními operacemi. Tyto výpočty se provádí v několika analytických centrech na světě a výslednými predikovanými souřadnicemi
jsou pak vážené průměry těchto několika řešení.
Cílem této diplomové práce, která byla psána za podpory výzkumného záměru MSM:210000007, je zamyslet se nad jednoduššími metodami
interpolace drah družic a posoudit jejich použitelnost v praxi. Dále poukázat na problematiku numerických výpočtů při interpolaci
v daných veličinách (terestrických souřadnicích resp. Keplerových dráhových elementech) a v závěru nastínit lepší postupy řešení
tohoto problému, než jakých jsem použil v předkládané práci.
Diplomová práce se tedy bude týkat jednak interpolace v terestrických souřadnicích družic GPS a jednak interpolace jejich
Keplerových dráhových elementů.
Původní ideou bylo, že praktickou použitelnost mnou realizovaných metod doložím srovnáním oficiálních predikovaných souřadnic,
mnou spočtených souřadnic družic GPS a jejich finálních hodnot. Nicméně výsledky výpočetních prací mě přivedly na myšlenku
nepočítat z Keplerových dráhových elemenů zpět terestrické souřadnice družice a tedy neprovádět výše zmíněné srovnání. Důvod
bude zřejmý z níže uvedených výsledků výpočtů. Pro úplnost jsou v příloze uvedena srovnání oficiálně predikovaných souřadnic
družic GPS s jejich finálními hodnotami.
Obsah:
| [0] Úvod | 1 |
| [0.1] Stručná historie | 1 |
| [0.2] Systém GPS-NAVSTAR | 1 |
| [0.3] Použitá symbolika v kapitolách [1.5] - [1.7] | 3 |
| [1] Teoretické základy | 4 |
| [1.1] Fourierova transformace | 4 |
| [1.2] Harmonická analýza Fourierovou řadou | 7 |
| [1.3] ITRS a rámec ITRF | 9 |
| [1.4] ICRS a rámec ICRF | 9 |
| [1.5] Transformace [x,y,z]ITRS à [x,y,z]ICRS | 10 |
| [1.5.1] Vliv precese | 11 |
| [1.5.2] Vliv nutace | 12 |
| [1.5.3] Vliv rotace Země – otočení o hvězdný čas | 14 |
| [1.5.4] Vliv pohybu pólu – volná nutace | 16 |
| [1.5.5] Časové systémy použité při výpočtech | 17 |
| [1.6] Výpočet stavových vektorů | 19 |
| [1.7] Transformace souřadnic [x,y,z]ICRS družice a její rychlosti na Keplerovy dráhové elementy |
20 |
| [1.8] Interpolace terestrických souřadnic [x,y,z]ITRS | 24 |
| [1.9] Interpolace Keplerových dráhových elementů | 27 |
| [1.9.1] Rektascenze výstupního uzlu dráhy družice - W | 28 |
| [1.9.2] Sklon dráhy družice – i | 29 |
| [1.9.3] Průvodič družice - r | 30 |
| [1.9.4] Argument deklinace dráhy družice - u | 31 |
| [2] Praktická realizace výpočtů | 32 |
| [2.1] Vstupní datové soubory a jejich struktura | 32 |
| [2.2] Interpolace terestrických souřadnic [x,y,z]ITRS | 34 |
| [2.3] Interpolace Keplerových dráhových elementů | 38 |
| [2.3.1] Rektascenze výstupního uzlu dráhy družice - W | 39 |
| [2.3.2] Sklon dráhy družice – i | 40 |
| [2.3.3] Průvodič družice - r | 41 |
| [2.3.4]Argument deklinace dráhy družice - u | 42 |
| [2.3.5] Výsledky výpočtů | 43 |
| [3] Závěr | 45 |
| [4] Použitá literatura | 49 |
| [5] Přílohy | 50 |
| [5.1] Příloha č.: 1 – Argumenty pro řešení nutace | 50 |
| [5.2] Příloha č.: 2 – Seznam řídících a monitorovacích stanic | 51 |
| [5.3] Příloha č.: 3 – Programy InterKPL a InterXYZ | 52 |
| [5.3.1] Program InterKPL | 53 |
| [5.3.2] Program InterXYZ | 58 |
| [5.4] Příloha č.: 4 – Obsah přiloženého CD | 59 |
| [5.5] Příloha č.: 5 – Srovnání oficiálních predikovaných souřadnic družice GPS PRN1 s jejich finálními hodnotami |
60 |
Zde bych rád napsal několik málo řádek o budování systému GPS NAVSTAR. To začalo v roce 1973 a bylo koncipováno jako obranný
navigační sytém Spojených Států Amerických. Vedením tohoto projektu bylo pověřeno U.S. Air Force (Letectvo Spojených Států).
Dále s touto institucí spolupracovalo U.S. Army Navy (Vojenské námořnictvo Spojených Států) a DMA (Defense Mapping Agency).
O pět let později, v roce 1978, se k tomuto projektu připojilo i dalších devět členských států NATO
(North Atlantic Treaty Organization).
Požadavky na vybudování takového navigačního systému byly, aby bylo možno v reálném čase kdykoliv a kdekoliv zjistit přesné
určení polohy (řádově do 10 m) libovolného počtu i rychle se pohybujících objektů.
Systém GPS-NAVSTAR (Global Positioning System – NAVigation System using Time
And Ranging) tvoří tři části: řídící, kosmická a uživatelská.
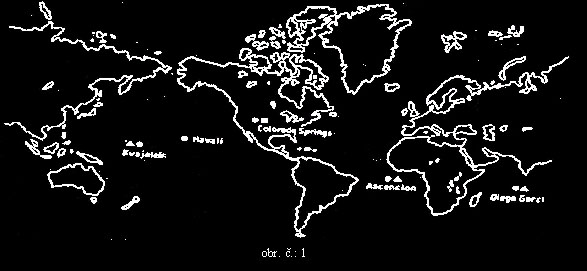
Řídící část tvoří sledovací stanice (obr. č.:1) rozmístěné po celé Zemi a hlavní řídící stanice (Colorado Springs), jež
zpracovává telemetrické informace a výsledky sledování pohybu družic z ostatních sledovacích stanic a přes jejich vysílače
tyto informace předává jednotlivým družicím spolu s povely pro řízení provozního režimu a korekcemi drah.
Kosmickou část tvoří nominálně 24 družic rovnoměrně rozmístěných na šesti oběžných drahách (obr. č.:2). Dráhy družic mají sklon 55o a jsou téměř kruhové. Výška družic nad povrchem Země je 20 183 km a jejich oběžná doba činí 11 hod 58 min, tedy 12 hvězdných hodin. Družice (obr. č.:3) mají hmotnost 845 kg a přibližné rozměry jsou 2,0 x 1,0 x 1,5 metrů. Životnost družic je počítána na 7,5 roku provozu. Palubní baterie jsou dobíjeny slunečními články o ploše 7,15 m2. Do družic se původně zabudovávaly rubidiové oscilátory, které jsou dnes nahrazovány oscilátory vodíkovými či cesiovými. Tyto oscilátory mají za úkol udržovat velmi přesné časové a kmitočtové informace.


A nakonec uživatelský segment. Ten je tvořen přijímači signálů GPS pomocí antén a registračních zařízení. Signál GPS tvoří
řada koherentních kmitočtů, které jsou odvozeny ze základní frekvence f0 = 10,23 MHz. Ta je ale kvůli kompenzaci
průměrného relativistického efektu snížena o 4,45 x 10-10 f0. Tento základní kmitočet je udržován
oscilátory na družicích s relativní přesností lepší než 10-13.
[0.3] Použitá symbolika v kapitolách [1.5] - [1.7]
| vektor, skalár (velikost vektoru) | |
| skalární součin | |
| vektorový součin | |
| Fj | Delauneyovy proměnné, j=(1, 2, …, 5) |
| z, q, z | precesní úhly |
| nutace v délce, nutace ve sklonu | |
| střední sklon ekliptiky | |
| g | střední anomálie Země |
| vektorový integrál ploch, jeho složky | |
| H | integrál energie, Hamiltonián |
| vektorový integrál Laplaceův, jeho složky | |
| T, V | kinetická energie družice, její silová funkce |
| GM | geocentrická gravitační konstanta |
| [r,u] | polární souřadnice družice v rovině její dráhy |
| m | hmotnost družice |
| geocentrický průvodič družice, jeho složky | |
| geocentrický průvodič družice, jeho složky | |
| vektor polohy družice, jeho složky | |
| platná relace | |
| vektor rychlosti družice, jeho složky | |
| b | výstupní uzel dráhy družice |
| W | rektascenze výstupního uzlu dráhy družice |
| e | excentricita dráhy družice |
| i | sklon dráhy družice |
| a | velká poloosa dráhy družice |
| v | pravá anomálie dráhy družice |
| E | excentrická anomálie družice |
| w | argument perigea dráhy družice |
| u | argument deklinace dráhy družice |
Pro interpolaci dat, kterou jsem v této práci prováděl, bylo nutné nejprve určit frekvence (resp. periody) a amplitudy
harmonických průběhů hodnot ať už reprezentovaných terestrickými souřadnicemi nebo přímo Keplerovými dráhovými elementy.
V některých případech tyto hodnoty (amplitudy a periody) lze vyčíst přímo z vynesených dat, nicméně tato transformace představuje
mnohem přesnější nástroj jak se těchto hodnot dopátrat.
Analýzu výchozích dat jsem prováděl v systému Matlab 4.0, který tuto transformaci po výpočetní stránce zajišťoval. Zde bych
chtěl jenom nastínit Fourierovu analýzu po teoretické stránce.
Mějme tedy definovanou funkci g(x), která splňuje podmínku absolutní integrovatelnosti:
![]()
a vyhovuje i ostatním Dirichletovým podmínkám. Tuto funkci chceme rozvinout do řady Fourierových funkcí:
1, cos(x), sin(x), cos(2x), sin(2x), …
což je systém funkcí, který je na intervalu <-p,p> ortogonální a tvoří bázi. Funkci g(x) tedy můžeme rozepsat do Fourierovy řady:
![]()
přičemž koeficienty ak a bk mají tvar:
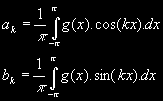
a říká se jim Fourierovy koeficienty. Ty vypočteme na základě MNČ minimalizací výrazu:
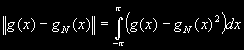
v němž funkce gN(x) má tvar:
![]()
Za použití Eulerových vzorců pro přechod ke komplexním číslům se rozvoj funkce g(x) ještě zjednoduší. Tyto vzorce mají tvar:
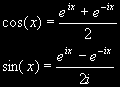
a původní báze se změní na bázi komplexních čísel:
1, eix, e-ix, e2ix, e-2ix, …
Potom funkci g(x) můžeme psát ve tvaru:
![]()
Koeficienty ck mají pak tvar:
![]() nebo jinak:
nebo jinak: 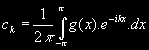
Až do této chvíle jsme se pohybovali pouze v intervalu <-p,p >. Nyní tento interval rozšíříme. A to substitucí proměnou tÎ <-N,N>. A dále:
![]() a po derivaci
a po derivaci ![]()
Změní se také Fourierovy koeficienty, které nabudou tvaru:
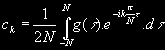
a rozvoj funkce g(x) bude vypadat takto:
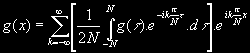
Logický požadavek je, aby se N à ¥. Proto zavedeme tuto symboliku:
![]() a dále
a dále ![]()
Tím rozvoj funkce g(x) přejde na tvar:
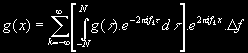
a pakliže vyjdeme z našeho požadavku aby N à ¥, musí Df à0 a dále sumační znak přejde na integrál a fk přejde na f. Tedy:

Výraz v hranatých závorkách označíme jako G(f). Takto dostáváme dvě funkce:
![]()
![]()
Funkce G(f) nazýváme Fourierovým obrazem nebo též spektrem dat. Funkce g(x) je pak nazývána jako zpětná Fourierova transformace. Originál (g(x)) a obraz (G(f)) nazýváme též Fourierovou dvojicí.
Problémem Fourierovy transformace je ale to, že tato není schopna detekovat takové periodické jevy, které mají frekvenci blížící se počtu měření. Nejlepších výsledků této transformace, ve smyslu důvěryhodnosti, se dosahuje v případech, kdy frekvence periodických jevů je menší než 1/2 počtu měření.
[1.2] Harmonická anlýza Fourierovou řadou
Používá se vykazují-li data jasnou periodicitu. Potom považujme interval od bodu x=a do bodu x=b, za nímž se průběh naměřených dat alespoň zhruba opakuje, za periodu P=b-a. Fourierova řada bude mít tedy tvar:
![]()
přičemž t je nová proměnná, která se získá z proměnné x transformací:
![]()
V obou posledně uváděných vztazích je index i={1,2,3,…,n}, kde n značí počet dat vstupujících do vyrovnání a je tedy shodný s počtem rovnic, ze kterých jsou pak následně počítány koeficienty interpolační funkce. Je dále výhodné Fourierovu řadu upravit (zjednoduší se derivace Fourierovy řady) pomocí substituce:
![]() ,
, ![]() ,
, ![]() , …
, …
na tvar:
![]()
Rovnice oprav tedy bude vypadat takto:
![]()
Úloha tak přejde na vyrovnání zprostředkujících měření, kde neznámé parametry jsou A0, A1, A2, B1, B2, C1, C2, …. Členy matice plánů A (design matrix A) pak tvoří parciální derivace Fourierovy harmonické řady:
![]()
Vektor neznámých je tedy dán vztahem:
![]()
kde h0 je vektor přibližných neznámých, vektor dh je roven výrazu:
![]() , který je dán podmínkou: vT.v à min
, který je dán podmínkou: vT.v à min
přičemž vektor l’ je vektor redukovaných měření a je roven:
![]() a
a ![]()
a to za předpokladu, že vektor oprav jednotlivých měření (v našem případě souřadnic resp. Keplerových dráhových elementů) je:
![]()
A dále zavedeme kovarianční matici neznámých parametrů:
![]()
potom střední chyby neznámých parametrů Fourierovy řady jsou dány vztahem:
![]()
Výraz m0 je odhad jednotkové střední chyby:
![]()
kde n je počet všech měření (v podobě jednotlivých souřadnic nebo Keplerových dráhových elementů) a k je počet nutných měření.
Souřadnice družic GPS tak jak jsou uváděny a publikovány v oficiálních datových souborech jsou v systému ITRS (International Terrestrial Reference System). Tento systém je realizován souřadnicemi bodů ITRF (International Terrestrial Reference Frame). Počátek tohoto referenčního rámce (frame) je definován v těžišti Země a to s přesností určení 10 cm. Referenční pól (je identický s osou Z kartézské soustavy) a referenční poledník (je identický s rovinou tvořenou osami XZ) jsou konzistentní s odpovídajícími směry systému BTS (BIH Terrestrial System, BIH – Bureau International de l’Heure) s přesností 0,003”. Osa X leží v nultém poledníku procházejícím Greenwichem a v rovině rovníku. BIH referenční pól byl připojen k CIO (Conventional International Origin) s přesností 0,03”.
Vzhledem k pohybům tektonických desek, jsou časové změny souřadnic bodů definujících rámec ITRF určovány kombinací přímého měření a teoretických hodnot vyšlých z modelů pohybů a to za podmínky tzv. NNR (No Net Rotation). Tj. za podmínky nulové rotace sítě, což odpovídá Tisserandově podmínce minimálního diferenciálního přírůstku kvadrátu momentu hybnosti.
Protože tento systém je pevně spjat s rotující Zemí, není systémem inerciálním.
Vzhledem k tomu, že Newtonův gravitační zákon platí v inerciálním systému a pohybové rovnice jsou v něm jednodušší (nemusí se zavádět korekce z neinerciality systému – zrychlení Eulerovo, Coriolisovo, dostředivé) je výhodné pro výpočet Keplerových dráhových elementů vyjít právě z onoho inerciálního systému. Takovým systémem je ICRS (International Celestial Reference System). Systém ICRS je realizován souborem mimogalaktických zdrojů elektromagnetického záření, tzv. kvasarů, které tvoří referenční rámec – ICRF (International Celestial Reference Frame) . Počátek ICRF je v barycentru sluneční soustavy. Osa Z kartézského souřadného systému směřuje do polohy středního rotačního pólu v epoše J2000.0. Osa X směřuje do Jarního bodu v epoše J2000.0 a osa Y doplňuje tento systém na pravoúhlý v matematicky kladném směru.
Zde bych chtěl uvést na pravou míru to, proč jsem jako inerciální systém označil systém ICRS. Pravda je ta, že přísně inerciální systém být ICRS nemůže a to proto, že je vázán na vesmírné objekty, které vykonávají svůj vlastní pohyb. Nicméně tento pohyb je vzhledem k obrovským vzdálenostem kvasarů tak malý, že, přihlédneme-li k naší přesnosti úhlového měření, chyby způsobené tímto zjednodušením jsou zanedbatelné.
[1.5] Transformace [x,y,z]ITRS à [x,y,z]ICRS
Abychom mohli spočítat Keplerovy dráhové elementy družic je nejprve nutné provést transformaci terestrických souřadnic družice na její hvězdné souřadnice. Tato transformace je realizována maticí rotace, které sestává z pěti dílčích matic rotace. Ty popisují vliv precese, nutace, rotace Země a pohybu pólu na terestrické souřadnice. Samotná transformace je dána vztahem:
![]()
a tedy

Precese je pohyb rotační osy Země okolo pólu ekliptiky a dále pohyb tohoto pólu vůči inerciální soustavě realizované rámcem ICRF.
Je to pohyb téměř věkovitý (sekulární) a dá se rozdělit na složku planetární a lunisolární. Lunisolární složka je způsobena Měsícem a Sluncem. Planetární složka, jak již název napovídá, je způsobena působením planet. Složku lunisolární nazveme lunisolární precesí a planetární složku nazveme analogicky planetární precesí.
Působením lunisolární precese (viz. obrázek č.:4) se střední světový pól pohybuje okolo pólu ekliptiky. Tento pohyb má periodu 25 800 let a říká se jí Platónský rok. Poloměr tohoto pohybu je roven sklonu ekliptiky vůči rovníku, a to 23,5o. Proto se mění i poloha jarního bodu a to o 50,3” za rok.
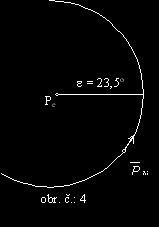
Planetární složka precese má pak za následek pohyb pólu ekliptiky vůči inerciální soustavě. Pohyb pólu ekliptiky je téměř kruhový s poloměrem 90’ a periodou 70000let. Vliv planetární precese je mnohem menší než lunisolární.
Precesní matice vyjadřující působení precese je součinem tří dílčích rotačních matic. Pro naplnění dílčích rotačních matic je třeba spočítat hodnoty precesních úhlů. Tyto úhly se počítají řadami, které jsou níže uvedeny. V těchto řadách se počítá s časovým intervalem T mezi danou epochou a epochou J2000.0 v Juliánských stoletích. Při výpočtu T by bylo správnější použít barycentrický dynamický čas (TBD). Ale pro naše účely postačí počítat s terestrickým dynamickým časem (TDT). Ten je s barycentrickým časem, až na periodické variace vůči času atomovému, shodný. Jeho výpočet je také jednodušší.
Výpočet terestrického dynamického času je dán vztahem:
![]()
TGPS se udává v MJD (Modifikované Juliánské Datum) a pak i TDT vyjde v MJD.
Výpočet precesních úhlů je dán řadami:

kde T je časový interval mezi danou epochou a epochou J2000.0 vyjádřen v juliánských staletích o délce 36525 dnů a je tedy dán vztahem:
![]()
Precesní matice má tvar:
![]()
Nutační pohyb je pohyb, který vykonává pravý (okamžitý) světový pól okolo středního světového pólu. Tento pohyb je způsoben periodickými změnami polohy Slunce a Měsíce vůči Zemi. Hlavni nutační perioda je 18,62 roku a její amplituda má hodnotu 9,21”. Schematicky vypadá nutační pohyb jak je ukázáno na obrázku č.:5.
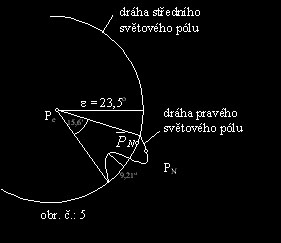
Nutace má dvě složky, nutaci v délce Dy a nutaci ve sklonu De. Nutace v délce je rozdíl mezi ekliptikální délkou ovlivněnou nutací a délkou nutací neovlivněnou. Nutace ve sklonu je rozdíl mezi sklonem roviny ekliptiky vůči rovině rovníku ovlivněné nutací a rovině rovníku neovlivněné nutací. Dále rozlišujeme ještě nutaci dlouhoperiodickou (složky Dy’ a De’) a krátkoperiodickou (složky dy a de).
Nutace v délce a nutace ve sklonu rozepsaná podle tohoto rozdělení mají tvar:
Dy = Dy’ + dy a De = De’ + de
Sklon roviny ekliptiky vůči rovině rovníku (střední sklon ekliptiky) je dán řadou:
![]()
kde je T časový interval mezi danou epochou a epochou J2000.0 vyjádřen v juliánských staletích o délce 36525 dnů a je tedy definován vztahem:
![]()
Další nutační parametry jsou dány řadami:
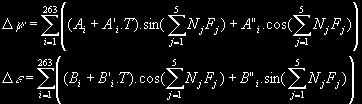
kde Fj jsou Delauneyovy proměnné, které postupně znamenají:
F1 = l = střední anomálie Měsíce
F2 = l’ = střední anomálie Slunce
F3 = F = L - W = střední délka Měsíce - střední délka výstupního uzlu
Měsíce
F4 = D = střední elongace Měsíce
F5 = W = střední délka výstupního uzlu Měsíce
Hodnoty Ai, Ai’, Ai”, Bi, Bi’, Bi”, Nj jsou uvedeny v příloze č.: 1. Delauneyovy proměnné jsou dány řadami, které jsou uvedeny v literatuře [2] na straně 101.
Nutační matice má tvar:
![]()
[1.5.3] Vliv rotace Země – otočení o hvězdný čas
Protože rámec ITRF je připojen k rotující Zemi, je třeba tyto souřadnice od ní “odpojit”. Přenásobíme-li tyto souřadnice příslušnou maticí rotace, získáme souřadnice, jejichž osa Z směřuje do pravého světového pólu v příslušné epoše.
Hvězdný čas, o který se bude soustava otáčet je čas GST (Greenwich Sideral Time), tedy Greenwichský hvězdný čas. Čas GST je závislý na časovém rozdílu mezi okamžikem výpočtu a epochou J2000.0. Je ale nutné tento časový rozdíl počítat v čase UT1, protože ten nejlépe odpovídá kolísavosti rychlosti rotace Země, jejíž velikost dosahuje řádově milisekund (viz. obr. č.:6).
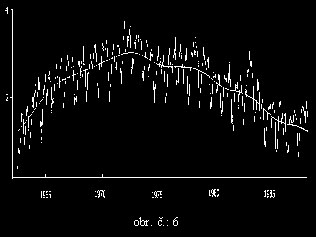
Předpokladem k tomuto výpočtu je znalost času TGPS. Tedy známe-li TGPS můžeme vypočítat UT1 pomocí tohoto vztahu:
UT1 = TGPS–(TGPS–UTC)+(UT1–UTC)
Hodnota (UT1–UTC) je udávána v souborech se souřadnicemi pólu (*.erp). Díky nepravidelnosti v rotaci Země i tato hodnota kolísá. Proto je službou IERS (International Earth Rotation Service) udržován tak, aby tato hodnota byla menší než je 1 vteřina.
Hodnota (TGPS-UTC) byla do 30.6.1997 včetně rovna:
(TGPS-UTC)= 11 sec.
Výpočet Greenwichského zdánlivého hvězdného času je dán vztahem:
![]()
kde výrazy Dy, De, e0
jsou nutační úhly počítané dle vztahů v kapitole [1.5.2] a hodnota
![]() je střední Greenwichský hvězdný čas v radiánech. Ten se vypočte dle následujících
vztahů a řad:
je střední Greenwichský hvězdný čas v radiánech. Ten se vypočte dle následujících
vztahů a řad:
![]()
kde písmenko c představuje korekci času pro UT1 ¹ 0:
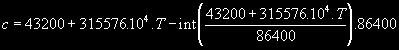
Hodnota časového rozdílu T (mezi danou epochou a epochou J2000.0) je počítána v čase UT1 v juliánských stoletích. Je dána vztahem:
![]()
A dále je třeba hodnotu SGM převést na radiány:
![]()
Rotační matice otočení o hvězdný čas bude mít tedy tvar:
![]()
[1.5.4] Vliv pohybu pólu – volná nutace
Vektor pravého světového pólu se nachází velmi blízko okamžitého vektoru rotace Země. Tato rotační osa mění stále svoji polohu v tělese Země a to způsobuje stálou změnu souřadnic pozorovacích míst na povrchu Země. Euler a později i Chandler stanovili, že pravý světový pól vykonává pohyb přibližně kruhový okolo hlavní osy setrvačnosti (pohyb bývá také nazýván volná nutace). Hlavní perioda tohoto pohybu je tzv. Chandlerova perioda a její naměřená hodnota činí 433 dnů. Maximální amplituda pohybu dosahuje hodnoty 0,25”. Pohyb rotační osy je znázorněn na obrázku č.:7.
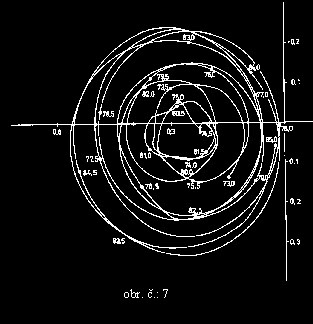
Aby nedocházelo ke stálým změnám souřadnic pozorovacích stanovisek na Zemi byl v letech 1900 – 1905 určen průměrný vektor rotace Země a do něj byla vložena osa Z systému ITRS. Takto stvořený pól je označován jako CIO (Convetional International Origin). Od tohoto vektoru se dále počítají souřadnice pravého (okamžitého) pólu.
Tyto souřadnice jsou určovány z měření VLBI (Very Long Baseline Interferometry), SLR (Satellite Laser Ranging) a GPS a bývají uváděny v bulletinech službou IERS.
Souřadnou soustavu v níž jsou uváděny souřadnice pravého pólu tvoří osa x - je vložena do směru Greenwichského poledníku a osa y - je vložena do směru poledníku o západní zeměpisné délce 90o.
Matice rotace vyjadřující pohyb pólu jsou následující:
![]()
![]()
[1.5.5] Časové systémy použité při výpočtech
Vzhledem k tomu, že jsem při řešení transformace mezi terestrickým systémem souřadnic a hvězdným systémem souřadnic použil hned několik časových systémů, považuji za vhodné se o nich zmínit ve zvláštní kapitole.
Časy, které jsem v této práci použil, ať již přeneseně nebo přímo, jsou časy rotační, dynamické a atomové.
Čas UT1 je časem rotačním a je použit pro výpočet matice otočení o hvězdný čas. A to proto, že, jak již bylo výše zmíněno, tento čas nejlépe vyhovuje nerovnoměrnostem v rotaci Země, způsobeným mnoha fyzikálními vlivy. Sekunda UT1 je kvůli těmto nerovnoměrnostem v rotaci Země delší než sekunda TAI (viz. dále), což se projevuje rozbíhavostí času rotačního a času atomového.
Čas TAI je atomový čas, který byl zaveden v roce 1967 a jehož jedna sekunda byla definována na základě záření atomu Cesia Cs 133. Počátek tohoto času byl určen tak, aby se shodoval s časem UT2 dne 1.1.1958. Velikost atomové sekundy byla stanovena tak, aby odpovídala efemeridové sekundě v roce 1900.
Čas UT2 je definován jako světový čas na okamžitém greenwichském poledníku zjištěný astronomickým měřením a opravený o pohyb pólu a vlivy sezónních variací v rychlosti rotace Země.
Čas UTC, který je použit v rozdílu (UT1-UTC), tabelovaném v souborech souřadnic pólu *.erp, je založen na základě času TAI. UTC je používán v občanském životě a je udržován v přibližné shodě s časem rotačním. To znamená, že rozdíl (UT1-UTC) je udržován tak, aby nepřekročil hodnotu 1s přičtením resp. odečtením právě jedné sekundy k resp. od času UTC. Časový rozdíl (UTC-TAI) činí dnes 32 sekund.
Dalším časovým systémem použitým při výpočtech je čas GPS, TGPS. Je založen na čase atomovém a byl definován tak, aby se v roce 1980 rovnal času UTC. Jeho rozdíl od času UTC je stálý a má hodnotu 19 sekund.
Dále byl použit časový systém TDT, tedy terestrický dynamický čas. Ten navazuje na efemeridový čas a platí, že 1.1.1977 0h 0m 0s TAI = 1.1.1997 0h 0m 32,184s TDT. Na základě tohoto vztahu lze tedy spočítat čas TDT při znalosti času atomového.
Barycentrický dynamický čas TDB nebyl při výpočtech použit, protože byl nahrazen časem TDT, který je výpočetně jednodušší a pro naše účely plně postačil. Nicméně i o něm bych se rád zmínil. Čas TDB se liší od času TDT pouze periodickými variacemi, které vyjadřují tyto vztahy:
![]()
přičemž g je střední anomálie Země a je dána vzorcem:
![]()
a T je časový interval mezi epochou J2000.0 a počítanou epochou v juliánských staletích.
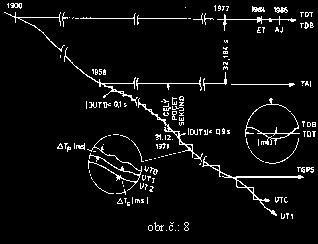
Obrázek č.:8 přehledně ukazuje vzájemné vztahy časových systémů, které jsem výše popsal.
[1.6] Výpočet stavových vektorů
Abychom mohli z hvězdných souřadnic spočítat Keplerovy dráhové elementy, je nutné určit nejprve tzv. stavové vektory. Stavový vektor definuje jak polohu družice v daném časovém okamžiku, tak i její rychlost.
Pro výpočet těchto vektorů jsem zvolil polynom stupně 12. To znamená, že pro výpočet jednoho vektoru bylo zapotřebí 13 časových okamžiků. Čas, pro který jsem vektor počítal se tedy nacházel uprostřed intervalu, který byl použit pro výpočet.
Stavové vektory jsem počítal pro týdenní data. Tj. pro pozorování, která pokrývají dobu 7 dnů a to po 15 minutách. Vzhledem k tomu, že pro výpočet jednoho vektoru je třeba 13 časových okamžiků, nebylo možné určit vektory pro prvních a posledních šest časů pozorování. To znamená, že celkový počet stavových vektorů byl 7x24x4-6-6=660.
Jako složku polohy stavového vektoru jsem vzal souřadnice družice v systému ICRS. Druhou složku vektoru, rychlost, jsem počítal jako derivaci polohy v daném čase a to pro každou souřadnici zvlášť. Konkrétní způsob jakým jsem vektory vypočetl je následující. Vektor měření (v našem případě souřadnice družice):
![]()
Vektor koeficientů funkce času je dán takto:
![]()
a konečně matice derivací funkce času je definována jako:
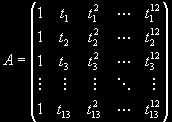
Pro větší numerickou stabilitu řešení byl výpočet prováděn v hodinách a kilometrech a zároveň sloupce 1-4 v matici A byly zvětšeny desetkrát. Vektor koeficientů h je tedy dán vztahem:
![]()
Pro souřadnice v daném časovém okamžiku (v tomto případě v časovém okamžiku t7) platí rovnice:
![]()
a pro rychlost družice v čase t7 je:
![]()
[1.7] Transformace souřadnic [x,y,z]ICRS družice a její rychlosti na Keplerovy dráhové elementy
Existuje šest Keplerových dráhových elementů, které odpovídají šesti integračním konstantám, tj. složkám vektorového integrálu ploch a složkám vektorového integrálu Laplaceovu. Dělí se na vnější dráhové elementy – rektascenze výstupního uzlu W, sklon roviny dráhy i, argument perigea w -(obr. č.:9) a vnitřní dráhové elementy – hlavní poloosa dráhy a, excentricita e, pravá anomálie n - (obr. č.:10).
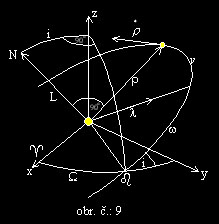
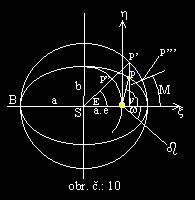
A pro transformaci do těchto dráhových elementů jsem zvolil postup, při němž se používá výpočtu právě zmíněných integrálů. Kromě toho se mi tento postup zdál, co do programového zajištění, nejvýhodnější.
Máme tedy šest počátečních podmínek. Jsou to souřadnice družice ![]() v systému ICRS
(definují její polohu) a složky rychlosti
v systému ICRS
(definují její polohu) a složky rychlosti ![]() v epoše t. Nejprve je vhodné
vypočítat pět integrálů. První tři jsou složky vektorového integrálu ploch a jsou dány vektorovým součinem vektoru polohy a
vektoru rychlosti:
v epoše t. Nejprve je vhodné
vypočítat pět integrálů. První tři jsou složky vektorového integrálu ploch a jsou dány vektorovým součinem vektoru polohy a
vektoru rychlosti:
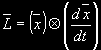
a v rozepsaném tvaru:
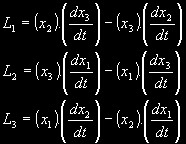
Dále je třeba vypočítat integrál energie, hamiltonián H. Ten plyne, v případě konzervativních soustav, ze zákona zachování energie.
H = T – V = konst.
kde T je kinetická energie družice o hmotnosti m:
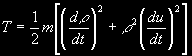
a V je její silová funkce:
![]()
přičemž [r,u] jsou polární souřadnice družice v rovině její dráhy. Úhel u je úhel měřený od polární osy o (směřuje do výstupního uzlu b
dráhy družice) ve směru pohybu družice.Vzhledem k posledním dvěma uvedeným vztahům je tedy hamiltonián H roven:
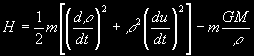
A vzhledem k tomu, že výraz v hranaté závorce je vlastně výrazem pro rychlost družice, můžeme psát:
![]()
a potom se bude hamiltonián H rovnat výrazu:
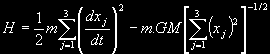
Posledním integrálem, který je třeba spočítat je vektorový integrál Laplaceův. Ten je definován vektorovým vztahem:
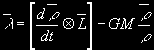
a rozepsán ve složkách má tvar:
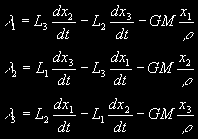
A nyní můžeme přejít rovnou na výpočet Keplerových dráhových elementů. Z vektorového integrálu ploch dostáváme hned několik výrazů pro výpočet rektascenze výstupního uzlu W a sklonu i:
![]()
![]()
![]()
![]()
![]()
Excentricitu můžeme spočítat podle vzorce:
![]()
Velká poloosa je dána vztahem:
![]() nebo také
nebo také ![]()
Pravou anomálii můžeme spočítat dle vzorce:
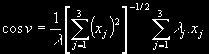
Posledním Keplerovým dráhovým elementem je argument perigea. Ten určíme na základě skalárního součinu Laplaceova vektoru
![]() a vektoru uzlové přímky (cos W; sin W; 0):
a vektoru uzlové přímky (cos W; sin W; 0):
![]()
Vzhledem k tomu, že dráhy družic GPS jsou téměř kruhové, bude výhodnější interpolovat argument deklinace u=w + n než samostatně argument perigea a pravou anomálii. Argument deklinace je dán vztahem:
![]()
Další úprava pro výpočty spočívá v tom, že nebudeme interpolovat hlavní poloosu dráhy družic (a tedy i jejich excentricitu), ale přímo průvodič družic:
![]()
přičemž excentrickou anomálii E spočteme ze vztahu:
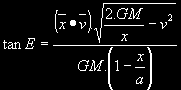
[1.8] Interpolace terestrických souřadnic [x,y,z]ITRS
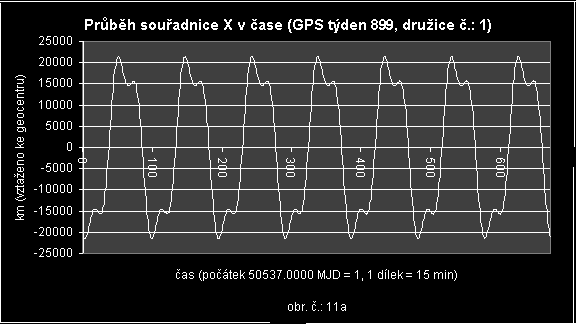
Vzhledem k časovému průběhu souřadnic (viz. obr. č.: 11a, 11b a 11c) jsem se rozhodl nepoužít polynomickou funkci, ale interpolaci pomocí Fourierovy harmonické řady. Ta je popsána v kapitole [1.2].
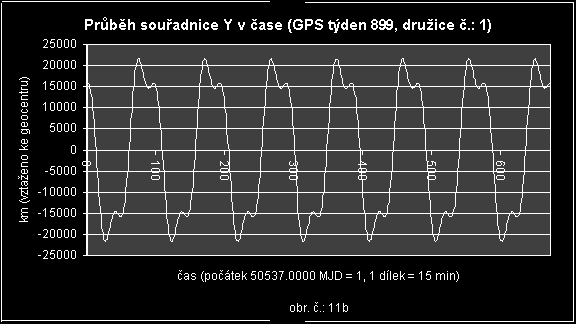
Z grafů (obr. č.: 11a, 11b) je patrné, že časová závislost dat, v tomto případě souřadnice X a Y, je součtem dvou periodicky se opakujících funkcí. Dále můžeme odhadnout periody obou funkcí (Ph je hlavní perioda a Pv je vedlejší perioda) a hlavní amplitudu. Vedlejší amplituda se z těchto grafů odhaduje velmi spatně. Číselné hodnoty těchto veličin jsou uvedeny v kapitole pojednávající o praktickém řešení jednotlivých problémů. Tyto hodnoty nejsou pouze odhadem, ale jsou podpořeny i analýzou pomocí Fourierovy transformace.
Avšak z informací, které nyní máme, můžeme sestavit interpolační funkci (pro interpolaci v souřadnicích X,Y), která by se co nejlépe přimykala danému časovému průběhu dat. Je to funkce:
![]()
kde neznámé jsou: a jako hlavní perioda, A je hlavní fázový posun, b je vedlejší perioda a konečně B je vedlejší fázový posun. Dále, jak je popsáno v kapitole [1.2], jsou t(1) a t(2) (čísla v závorkách nejsou mocniny, ale indexy odlišující od sebe obě proměnné) nové proměnné, které dostaneme z původních proměnných x takto:
![]() a
a ![]()
Využijeme nyní součtový vzorec pro součet argumentů ve funkci sinus a dále zavedeme substituci:
![]() ,
, ![]()
Potom bude konečný tvar interpolační funkce tento:
![]()
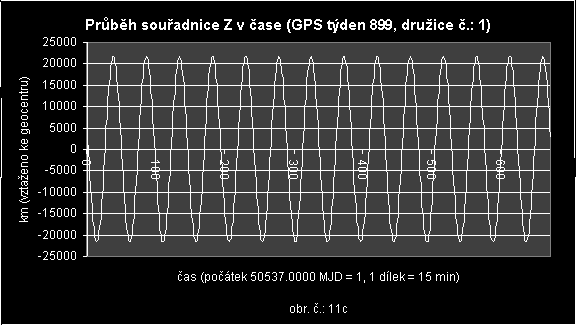
Je zřejmé, že funkce pro interpolaci v souřadnicích Z (obr. č.: 11c) bude jednodušší. Bude obsahovat pouze první člen Fourierovy harmonické řady. Její odvození zde ale uvádět nebudu, neboť je naprosto analogické s výše odvozenou funkcí pro souřadnice X a Y, s omezením na jeden člen řady. Konečný tvar tedy bude:
![]()
kde
![]()
[1.9] Interpolace Keplerových dráhových elementů
Interpolační funkce dráhových elementů jsou součtem dvou dílčích funkcí. Jsou to funkce polynomické (v některých případech i konstantní), které vystihují trend dráhových elementů po dobu, kterou zabírají analyzovaná data (jeden GPS týden), a pak jsou to funkce harmonické, které vystihují harmonický časový průběh dráhových elementů samotných.
V některých případech je použita funkce polynomická pro vystižení týdenního trendu, ale ve skutečnosti, vezmeme-li v potaz data většího časového úseku než jeden týden, přejde tento trend na funkci harmonickou, jejíž perioda je mnohem větší než právě jeden týden. A dlouhodobý časový vývoj dráhových elementů by pak měl ještě další průběhy.
Konečné podoby interpolačních funkcí uvedené v této kapitole jsou výsledkem několikadenních pokusů o co nejlepší vystižení průběhu časové závislosti dráhových elementů za použití analýzy pomocí Fourierovy transformace. V kapitole [1.9] a v jejích podkapitolách budu uvádět konečné tvary interpolačních funkcí, které budou komentovány na základě grafů časových průběhů jednotlivých dráhových elementů. Komentáře založené na analýze pomocí Fourierovy transformace budou uvedeny dále v textu v kapitole [2.3], která se týká praktických výpočtů a mezivýsledků. Tam také budou uvedeny číselné hodnoty period a amplitud jednotlivých harmonických průběhů.
Ještě je třeba podotknout, že pro praktickou část této práce, tedy pro výpočty, jsem si náhodným výběrem zvolil družici PRN1. Nicméně vše co je v této práci uvedeno platí i pro všechny ostatní družice GPS. Výpočty byly prováděny ještě pro některé další družice. Výsledky výpočtů ale nemohu uvádět a to z toho důvodu, že by tato práce nabyla ohromných rozměrů.
[1.9.1] Rektascenze výstupního uzlu dráhy družice - W
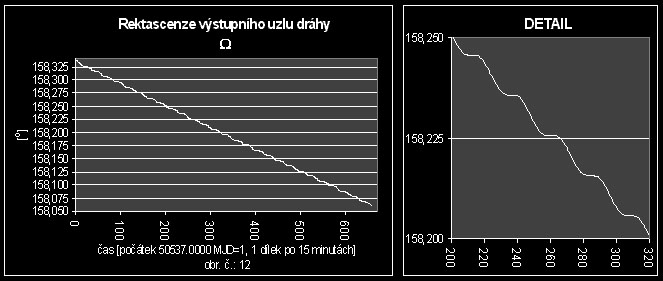
Z grafu časového průběhu W (obr. č.: 12) je zřejmé, že interpolační funkce bude mít tvar součtu funkce lineární a harmonické. Dále je vidět, a Fourierova transformace to potvrdila, že zde figuruje pouze jedna harmonická funkce (s periodou P a že tedy ve výsledné interpolační funkci bude jen jeden harmonický člen.
Interpolační funkce tedy bude vypadat takto:
![]()
Pomocí součtového vzorce pro součet argumentů funkce sinus a substituce:
![]()
a po příslušných úpravách dostáváme konečnou podobu interpolační funkce:
![]()
přičemž t bude rovno výrazu:
![]()
[1.9.2] Sklon dráhy družice - i
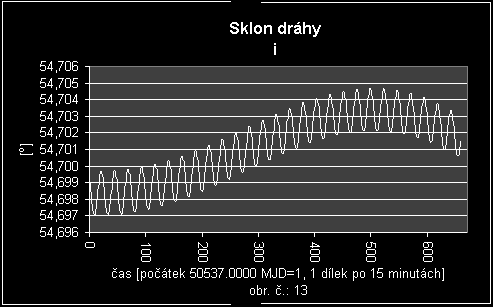
Jak je vidět z týdenních dat (obr. č.:13) má sklon dráhy družice průběh harmonický. Funkce, která by se nejlépe přiblížila tomuto průběhu by vypadala jako součet dvou harmonických funkcí o různých periodách. Nicméně hlavní perioda tohoto časového průběhu je delší než jeden týden a proto funkce, kterou jsem nakonec zvolil jako interpolační je součtem kubické polynomické funkce a harmonické funkce (s periodou P) s jedním harmonickým členem. Konečný tvar interpolační funkce tedy je:
![]()
Součtovým vzorcem pro součet argumentů funkce sinus a zavedením substituce:
![]()
získáme finální podobu funkce:
![]()
přičemž t bude opět rovno výrazu:
![]()
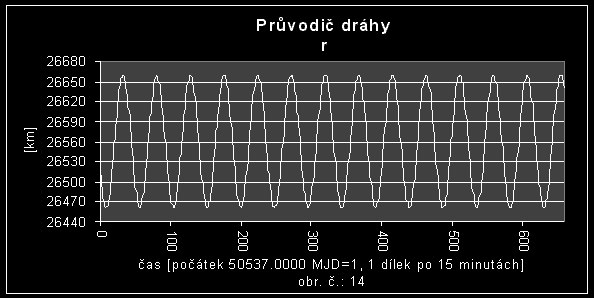
Již z grafu časového průběhu velikosti průvodiče dráhy družice (obr. č.:14) je vidět, že interpolační funkce bude velmi jednoduchá. Trend tohoto časového průběhu průvodiče je konstantní. Je zřejmé, že v harmonickém průběhu figuruje pouze jedna frekvence s periodou Ph a amplitudou b.
Výsledná podoba interpolační funkce tedy je:
![]()
kde b je zmiňovaná hlavní amplituda, B je patřičný fázový posun a t je nová proměnná získaná transformací:
![]()
Za využití již výše několikrát zmíněného součtového vzorce a substituce:
![]()
dostaneme po jednoduchých úpravách interpolační funkci ve tvaru:
![]()
[1.9.4] Argument deklinace dráhy družice - u
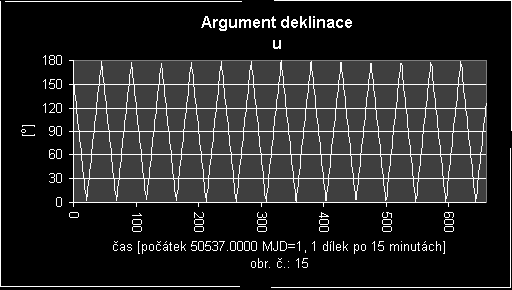
Z grafu (obr. č.:15) je patrné, že argument deklinace je veličinou (stejně jako průvodič), která vykazuje největší změny své velikosti v čase. A nejen největší ale také nejostřejší. Závislosti, kterou můžeme pozorovat ve výše zmíněném grafu, nejlépe tvarově vyhovuje pilovitá funkce, která je dána součtem řady:
![]()
z níž pro náš účel bohatě postačí první tři členy této řady. Koeficient a vyjadřuje konstantní trend časové závislosti, koeficient b je pak její amplituda a B má význam fázového posunu. Proměnná t je pak opět nová proměnná vzniklá transformací, která má tvar:
![]()
Následují analogické substituce a analogické úpravy jako v předcházejících podkapitolách kapitoly [1.9], po nichž získáme konečnou podobu interpolační funkce:
![]()
[2] Praktická realizace výpočtů
V této kapitole popíši postupy výpočtů, uvedu dílčí i konečné výsledky a okomentuji časové závislosti na základě analýzy dat pomocí Fourierovy transformace. Závěr a komentáře výsledků pak budou uvedeny v kapitole [3].
Dále zde budou uvedeny ukázky datových souborů se souřadnicemi družic a souřadnicemi pólu a jinými důležitými parametry vstupujícími do výpočtů. Popíši zde také způsob, kterým jsem získal data potřebná pro výpočetní práce.
Pro úplnost bych chtěl podotknout, že, kromě Fourierových transformací (ty jsem počítal v programu Matlab 4.0), jsem vše počítal na software, který jsem si sám naprogramoval v jazyce C++ za použití vývojového prostředí C++ Builder v3.0. Zdrojové kódy, programové soubory (*.exe) a další dokumenty týkající se této práce jsou přiloženy na CD. Popis programů je v příloze č.:3.
[2.1] Vstupní datové soubory a jejich struktura
Datové soubory, které obsahují potřebné informace jsem získal pomocí Internetu a služby FTP (File Transfer Protocol) a to z vládního serveru organizace NASA (National Aeronautic and Space Administration – Národní správa pro letectví a kosmický prostor) v USA. Adresa serveru je: cddis.gsfc.nasa.gov a adresář, kde se data nacházejí je: gps3:[products]/”week”, kde “week” je číslo týdne (například: 0899), který nás zajímá.
V těchto adresářích se tedy dají najít jak soubory s predikovanými, tak i s finálními souřadnicemi družic a také predikované a finální souřadnice pravého pólu v soustavě CIO (viz. kapitola [1.5.4]).
Soubory s predikovanými souřadnicemi družic se jmenují IGPxxxxy.sp3 a soubory s finálními souřadnicemi družic se jmenují IGSxxxxy.sp3 a dále soubor s finálními souřadnicemi pravého pólu má jméno IGSxxxx7.erp a soubory s predikovanými souřadnicemi pravého pólu se jmenují IGPxxxxy.erp. Písmena v názvech souborů mají tento význam:
xxxx - číslo GPS týdne (například 0899)
y - číslo dne v týdnu od 0=neděle až do 6=sobota
Každý ze souborů má svou “hlavičku” a strukturované “tělo”. Příklad “hlavičky” souboru souřadnic družic je následující:
#aP1997 3 30 0 0 .00000000 96 ORBIT ITR94 HLM IGSÚdaje které byly pro mne důležité a které lze vyčíst z této “hlavičky” jsou:
datum: 30.3.1997
souřadný systém: ITRF94, zpracováno HLM IGS
čas: .00000 sekunda týdne 899 (neděle)
Dalšími údaji jsou počet zpracovávaných družic (25), jejich PRN (Pseudo Random Nubers - pseudonáhodná čísla), MJD týkající se půlnoci daného dne, tedy 30.3.1997 0h 0m 0s.
Tělo souboru se souřadnicemi družic má pevně stanovenou strukturu. Ta je velmi dobře patrná z ukázky:
* 1997 3 30 0 0 .0000Jsou zde uvedeny PRN jednotlivých družic pro daný okamžik (30.3.1997, 0h 0m 0s = 50537.0000 MJD), který je uveden v prvním řádku každého bloku a je označen “*”, dále blok obsahuje souřadnice družic, které jsou seřazeny dle PRN a korekci jejich hodin v mikrosekundách. Bloky jsou seřazeny v časové souslednosti vždy po 15 minutách.
Datový soubor s finálními souřadnicemi pravého pólu a korekcí (UT1-UTC) má tuto strukturu:
Source: Xpole,Ypole,Xrt,Yrt: weighted average of centres;Informace, které byly pro řešení daných problémů potřebné jsou: MJD a pro něj uváděné souřadnice pólu v soustavě CIO a korekce hodin (UT1-UTC). Z dalších informací obsažených v tomto souboru uvedu například rozdíl aktuální délky dne a 24 hodin v sekundách, charakteristiky přesnosti souřadnic pólu, rozdílu (UT1-UTC), délky dne (LOD).
[2.2] Interpolace terestrických souřadnic [x,y,z]ITRS
V kapitole [1.8] jsem se odvolával na Fourierovu transformaci jako na nástroj mnohem přesnějšího určení frekvencí, period a amplitud harmonických časových průběhů dat. Fourierovy transformace tedy pro jednotlivé terestrické souřadnice vypadají takto:
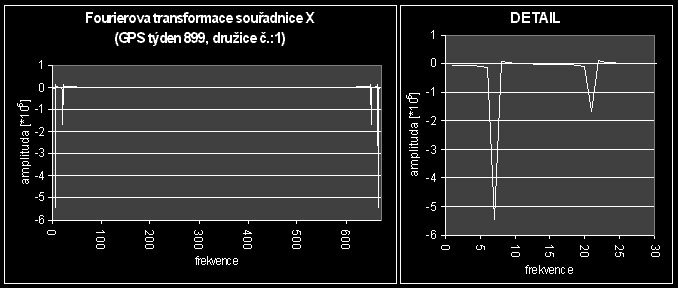
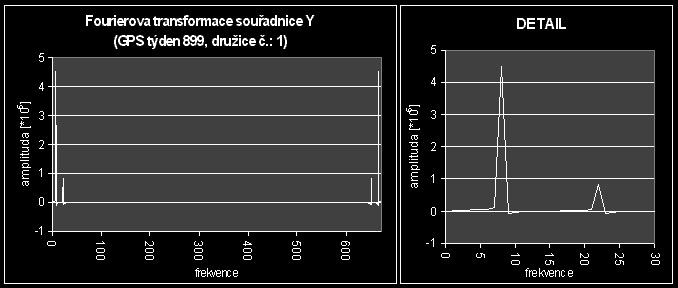
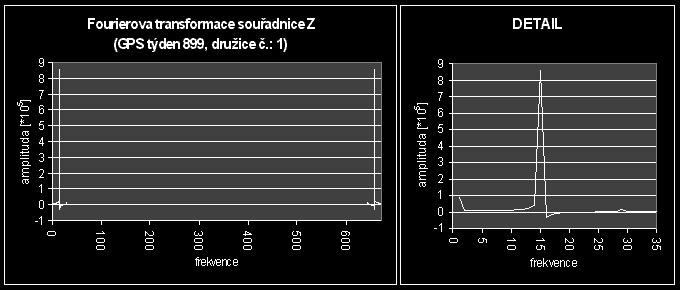
Informace, které z těchto grafů (a z grafů na obr. č.:11a, 11b, 11c) můžeme vyčíst je možné sestavit do tabulky:
| souřadnice | X |
Y |
Z |
|
frekvence |
hlavní |
7 |
7 |
14 |
vedlejší |
21 |
21 |
--- |
|
perioda |
hlavní [měř.] |
96 |
96 |
48 |
vedlejší [měř.] |
32 |
32 |
--- |
|
amplituda |
hlavní [km] |
20880 |
20880 |
21600 |
tab.: 1 |
vedlejší [km] |
5540 |
5540 |
--- |
Hodnoty v tabulce a odečtené přibližné fázové posuny z grafů na obr. č.:11a, 11b, 11c byly použity pro výpočet přibližných koeficientů aproximačních funkcí, které jsou uvedeny v kapitole [1.8].
Z grafů Fourierových transformací jednotlivých souřadnic družic je dále vidět to, že dochází k velmi ostrým změnám hodnot souřadnic. To je patrné z toho, že píky ostatní signál (na časový průběh souřadnic se můžeme dívat jako na určitý signál) výrazně převyšují. Přechody mezi píky a ostatním signálem jsou velmi ostré a úzké. To znamená, že časový průběh souřadnic není zatížen náhodnými rušivými vlivy, tzv. šumem, a je tedy z pohledu signálu poměrně čistý.
Matice plánu byla sestavena z parciálních derivací interpolačních funkcí dle jednotlivých neznámých, tedy koeficientů interpolačních funkcí. Vektor neznámých pak tvoří jednotlivé koeficienty těchto funkcí (viz. aplikace kapitoly [1.2]). Výsledné vektory neznámých parametrů interpolačních funkcí a odhady jejich středních chyb jsou sestaveny v tabulkách č.:2a, 2b, 2c.
| tab.: 2a | souřadnice X |
|
neznámé |
hi [km] |
mhi [km] |
A1 |
-15280,46 |
255,90 |
A2 |
-14235,64 |
255,90 |
B1 |
-5360,39 |
255,90 |
B2 |
1414,43 |
255,90 |
| tab.: 2b | souřadnice Y |
|
neznámé |
hi [km] |
mhi [km] |
A1 |
14437,66 |
258,49 |
A2 |
-15274,42 |
258,49 |
B1 |
1420,67 |
258,49 |
B2 |
5451,62 |
258,49 |
| tab.: 2c | souřadnice Z |
|
neznámé |
hi [km] |
mhi [km] |
A1 |
5335,97 |
422,51 |
A2 |
-20925,84 |
422,51 |
Z hodnot v tabulkách 2a, 2b a 2c jsem dále vypočítal původní koeficienty interpolačních funkcí pomocí umocnění a sečtení resp. podělení substitučních výrazů, které jsou popsány v kapitole [1.8]. Číselné hodnoty koeficientů jsou přehledně uspořádány do tabulek:
souřadnice X |
||
neznámé |
hi |
mhi |
a [km] |
20884,106 |
255,900 |
A [rad] |
3,962374351 |
0,012253337 |
b [km] |
5543,861 |
255,900 |
B[rad] |
4,970375753 |
0,046159167 |
souřadnice Y |
||
neznámé |
hi |
mhi |
a [km] |
21017,943 |
258,490 |
A[rad] |
2,384349331 |
0,012298539 |
b [km] |
5633,690 |
258,490 |
B[rad] |
0,2549261762 |
0,045882893 |
souřadnice Z |
||
neznámé |
hi |
mhi |
a [km] |
21595,448 |
422,510 |
A [rad] |
2,891919021 |
0,019564772 |
[2.3] Interpolace Keplerových dráhových elementů
K analýze Keplerových dráhových elementů opět použiji Fourierovu transformaci. Na základě interpretace grafů této transformace a grafů časových průběhů jednotlivých dráhových elementů určíme přibližné hodnoty jednotlivých koeficientů interpolačních funkcí a kromě toho nám též pomůže zjistit teoretickou použitelnost této metody pro určení predikovaných souřadnic družic na základě určení interpolačních funkcí Keplerových dráhových elementů a jejich koeficientů.
Kapitola je rozdělena do jednotlivých podkapitol, v nichž jsou popsány grafy Fourierových analýz Keplerových dráhových elementů. Dále jsou v podkapitolách uvedeny frekvence, periody a amplitudy Keplerových dráhových elementů. V poslední podkapitole jsou pak uvedeny tabulky s výslednými hodnotami koeficientů jednotlivých interpolačních funkcí a jejich středními chybami.
[2.3.1] Rektascenze výstupního uzlu dráhy družice - W
Graf Fourierovy transformace časového průběhu rektascenze výstupního uzlu dráhy družice má tuto podobu:
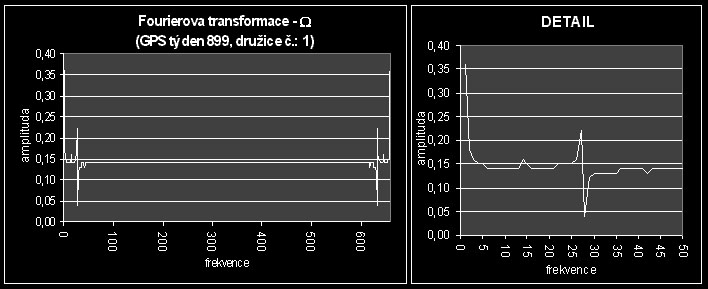
Z tohoto grafu a z grafu na obr. č.:12 je možné vyčíst tyto důležité informace:
Keplerův dráhový element |
W |
|
frekvence |
hlavní |
1 |
vedlejší |
27 |
|
perioda |
hlavní [měř.] |
--- |
vedlejší [měř.] |
24 |
|
amplituda |
hlavní [o] |
--- |
tab.: 3 |
vedlejší [o] |
0,0016 |
Vzhledem k tomu, že píky nad ostatním pozadím signálu (opět se na časový průběh Keplerových dráhových elementů můžeme dívat jako na jistý signál a danou periodou, frekvencí a amplitudou) nejsou příliš převýšeny, můžeme konstatovat, že časová změna hodnot rektascenze výstupního uzlu dráhy družice nenabývá závratných velikostí. Dále je možné říci, že časový průběh této veličiny není zatížen šumem a je tedy poměrně čistý. To je patrné z toho, že přechody do píků jsou ostré.
Rád bych ještě okomentoval tu skutečnost, že Fourierova transformace odhalila ještě jednu frekvenci, jejíž perioda je vzhledem k týdennímu časovému intervalu dat dlouhodobá. Jedná se s největší pravděpodobností a kombinaci jevů, které mají periodu cca. 14 a 28 dní a amplitudu v součtu okolo 9”. Tyto jevy se ale v mých výpočtech neuplatní, neboť mají na rektascenzi výstupního uzlu v horizontu jednoho týdne nepatrný vliv.
[2.3.2] Sklon dráhy družice - i
Na obrázku č:13 můžeme vidět časový průběh sklonu dráhy družice, jehož graf Fourierovy transformace vypadá takto:
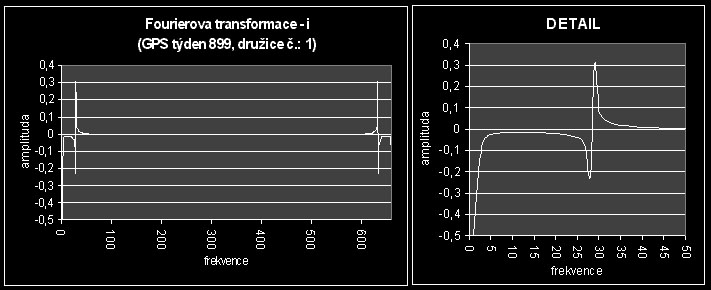
Opět nejprve uvedu tabulku (tab. č.:4) s hodnotami frekvencí, period a amplitud jevů, které odhalila Fourierova analýza a graf časového průběhu sklonu dráhy družice:
Keplerův dráhový element |
i |
|
frekvence |
hlavní |
1 |
vedlejší |
27 |
|
perioda |
hlavní [měř.] |
--- |
vedlejší [měř.] |
24 |
|
amplituda |
hlavní [o] |
--- |
tab.: 4 |
vedlejší [o] |
0,0013 |
Fourierova transformace odhalila i zde jev, který má frekvenci 1 (má delší periodu než týden). Tento jev jsem již popsal v kapitole [1.9.2] a je to právě ten trend, který jsem nahradil kubickým polynomem. Vzhledem k týdennímu časovému horizontu dat je tento trend dlouhodobější. Nicméně s ním bylo nutno počítat, protože jeho amplituda má velikost 9” (perioda činí 14 dní).
Ani v tomto případě píky podstatně nepřevyšují ostatní pozadí signálu. To znamená, že amplituda harmonického průběhu hodnot této veličiny nebude velká a že nebude docházet k dramatickým změnám hodnot této veličiny v čase. Nicméně je vidět, že průběh sklonu dráhy družice v čase je mírně zatížen náhodnými rušivými vlivy, tzv. šumem, protože přechod mezi píkem a pozadím signálu je poměrně pozvolný.
Fourierova transformace této veličiny je znázorněna na následujícím grafu:
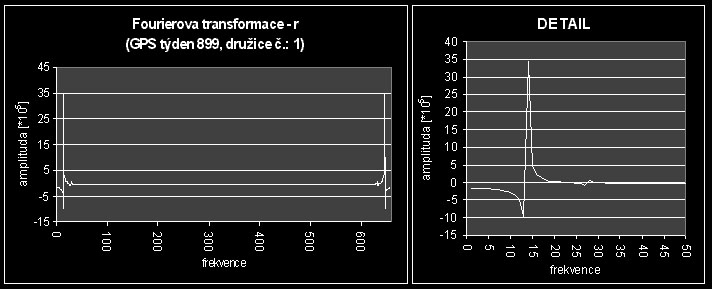
Na základě této Fourierovy transformace a za pomoci obrázku č.:14 jsem stanovil tyto hodnoty frekvence, periody a amplitudy časového průběhu průvodiče:
Keplerův dráhový element |
r |
|
frekvence |
hlavní |
14 |
perioda |
hlavní [měř.] |
48 |
amplituda |
hlavní [km] |
99,408 |
Z grafu Fourierovy transformace lze vyčíst periodický průběh s periodou 48 měření (po 15 minutách) a amplitudou 99,408 km. Dále z grafu Fourierovy transformace můžeme usoudit na to, že dochází k velkým změnám hodnot této veličiny v čase, protože pík velmi převyšuje pozadí signálu. Dále přechod mezi píkem a pozadím signálu není ostrý, ale poměrně pozvolný. Můžeme tedy říci, že časový průběh hodnot této veličiny je mírně zatížen šumem.
[2.3.4] Argument deklinace dráhy družice - u
Graf Fourierovy transformace je vyobrazen na obrázku:
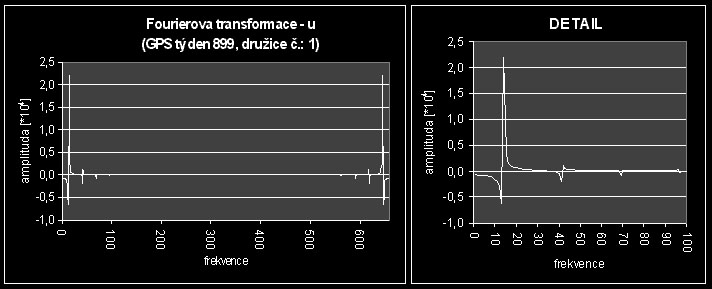
Z grafu Fourierovy transformace argumentu deklinace je na první pohled zřejmé, že zde dochází k velmi rychlým a velkým změnám hodnot této veličiny v čase, protože zde píky dosahují značných hodnot. Dále vidíme, že přechod mezi píkem a zbylým pozadím není ostrý a proto můžeme konstatovat, že hladký průběh bude mírně zatížen šumem. Tento šum ovšem nedosahuje takových hodnot, aby velkou měrou ovlivňoval výsledky interpolace této veličiny. Je zde evidentní jedna frekvence o hodnotě 14, jejíž amplituda mnohonásobně převyšuje ostatní píky, které jsou mimo jiné také důkazem přítomnosti šumu, o kterém jsem se zmínil výše v tomto odstavci a jímž je zatíženo pozadí signálu.
Hodnoty, které jsem vyčetl jak z Fourierovy transformace tak i z grafu časového průběhu pravé anomálie jsou uvedeny v následující tabulce:
Keplerův dráhový element |
u |
|
frekvence |
hlavní |
14 |
perioda |
hlavní [měř.] |
48 |
amplituda |
hlavní [o] |
89,7 |
V této kapitole budou uvedeny a přehledně do tabulek vepsány výsledky výpočtů koeficientů interpolačních funkcí, které jsou popsány v kapitole [1.9]. Pro stanovení přibližných hodnot těchto koeficientů jsem použil nejen hodnoty uvedené v kapitole [2.3], ale také odhady fázových posunů jednotlivých časových závislostí. Tyto posuny jsou velmi dobře patrné z grafů časových závislostí (obrázky č.:12-15) a proto jsem je do tabulek neuváděl. Tam kde tyto posuny patrné přímo nebyly, byl jsem odkázán pouze na jejich odhad. Nicméně do výpočtu přibližných koeficientů jsou tyto posuny zahrnuty.
Výsledky, ke kterým jsem při výpočtech došel tedy jsou:
Keplerovy dráhové elementy |
|||||
W |
i |
||||
h [rad] |
mh [rad] |
h [rad] |
mh [rad] |
||
a= |
-7,23444733E-6 |
1,865367182E-9 |
a= |
-1,61863788E-12 |
1,874316E-14 |
b= |
2,763452744 |
7,116319521E-7 |
b= |
1,320797908E-9 |
1,884701061E-11 |
C1= |
2,371446143E-5 |
5,026123326E-7 |
c= |
-8,295882344E-8 |
5,363703836E-9 |
C2= |
1,384354289E-5 |
5,026777371E-7 |
d= |
0,9546683787 |
4,097804064E-7 |
E1= |
1,098019246E-5 |
1,440156275E-7 |
|||
E2= |
-1,929642108E-5 |
1,441275214E-7 |
|||
Keplerovy dráhové elementy |
|||||
r |
u |
||||
h [m] |
mh [m] |
h [rad] |
mh [rad] |
||
a= |
26561121,466349 |
191,188433 |
a= |
1,5731639219 |
0,0028268662 |
B1= |
-50754,690849 |
270,572742 |
B2= |
-0,6484541852 |
0,0039945568 |
B2= |
-84941,615005 |
270,153519 |
B1= |
1,0919048630 |
0,0040007570 |
C2= |
0,1375101445 |
0,0039941617 |
|||
C1= |
0,0047597538 |
0,0040001698 |
|||
D2= |
-0,0205526854 |
0,0039938277 |
|||
D1= |
-0,0435551059 |
0,0039999081 |
|||
Dále jsem spočetl původní koeficienty v interpolačních funkcích z nichž jsem vycházel v kapitolách [1.9.1] až [1.9.4] a to umocněním a sečtením, popřípadě podělením, jednotlivých substitučních výrazů. Výsledné hodnoty koeficientů s odhady jejich středních chyb jsou sestaveny v následujících tabulkách:
Keplerovy dráhové elementy |
|||||
W |
i |
||||
h [rad] |
mh [rad] |
h [rad] |
mh [rad] |
||
a= |
-7,23444733E-6 |
1,865367182E-9 |
a= |
-1,61863788E-12 |
1,874316E-14 |
b= |
2,763452744 |
7,116319521E-7 |
b= |
1,320797908E-9 |
1,884701061E-11 |
c= |
0,000027459413 |
0,00000050262 |
c= |
-8,295882344E-8 |
5,363703836E-9 |
C= |
1,042403945 |
0,01830560308 |
d= |
0,9546683787 |
4,097804064E-7 |
e= |
0,0000222017228 |
0,0000001441002 |
|||
E= |
2,624258519818 |
0,006487920134 |
|||
Keplerovy dráhové elementy |
|||||
r |
u |
||||
h |
mh |
h [rad] |
mh [rad] |
||
a [m]= |
26561121,466349 |
191,188433 |
a= |
1,5731639219 |
0,0028268662 |
b [m]= |
98950,071766 |
270,263878 |
b= |
1,5667263831 |
0,0032415819 |
B [rad]= |
4,1737917338 |
0,0016892822 |
B= |
2,1066994269 |
0,0046009995 |
Veškeré číselné hodnoty výpočtů koeficientů interpolačních funkcí jsou uvedeny v příslušných tabulkách v kapitolách [2.2] a [2.3.5]. V této kapitole bych rád okomentoval praktickou použitelnost těchto dvou metod, kterými jsem se v diplomové práci zabýval.
Výsledky výpočtů uvedené v kapitole [2.2] ukazují přímo střední chyby s jakými by byly určeny souřadnice družice PRN1 z vypočítaných vyrovnaných koeficientů interpolačních funkcí. Jejich velikosti jsou:
mx = 361,9 km
my = 365,6 km
mz = 422,5 km
Pro zjištění odhadů středních chyb souřadnic družice PRN1 interpolovaných na základě Keplerových dráhových elementů je třeba malého zamyšlení. Transformace Keplerových dráhových elementů na kartézské souřadnice v systému ICRS je dána těmito vzorci:
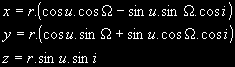
Podívejme se jak budou vypadat parciální derivace souřadnice x (u ostatních souřadnic jde o analogii a proto se budu v těchto rozborech zabývat pouze souřadnicí x) podle jednotlivých veličin:
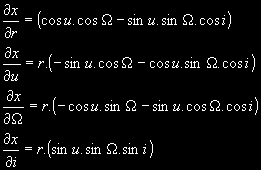
Podle zákona hromadění středních chyb platí:
![]()
Podívejme se, jakým dílem, z celkové střední chyby souřadnice x, přispěje, při zanedbání středních chyb všech ostatních veličin, střední chyba argumentu deklinace. Zaveďme několik předpokladů. Hodnoty rektascenze výstupního uzlu dráhy a sklonu dráhy družice můžeme pro účely našeho odhadu brát jako konstanty. Jedinou proměnnou veličinou je pro nás argument deklinace. V závislosti na jeho hodnotě závorka v parciální derivaci dosahuje v druhé mocnině hodnoty až 0,908. Dále pro účely tohoto odhadu postačí vzít jako velikost průvodiče hodnotu r = 26560 km. Odhad střední chyby argumentu deklinace je mu = 0,00748 rad. A při maximální velkosti závorky ve výrazu parciální derivace je hodnota, kterou přispívá střední chyba argumentu deklinace k celkové velikosti střední chyby souřadnice x, rovna 189,3 km. Vlivy středních chyb ostatních veličin jsou i o několik řádů menší.Shrnu-li tyto výsledky, musím konstatovat, že střední chyby souřadnic družic určené jak na základě interpolace v terestrických souřadnicích tak i na základě interpolace v Keplerových dráhových elementech jsou velmi velké.
Pro porovnání původních dat s interpolovanými jsem použil jako demonstračního příkladu argumentu deklinace (obr. č.: 16), ale podobně by vypadaly i grafy srovnání ostatních Keplerových dráhových elementů a terestrických souřadnic.
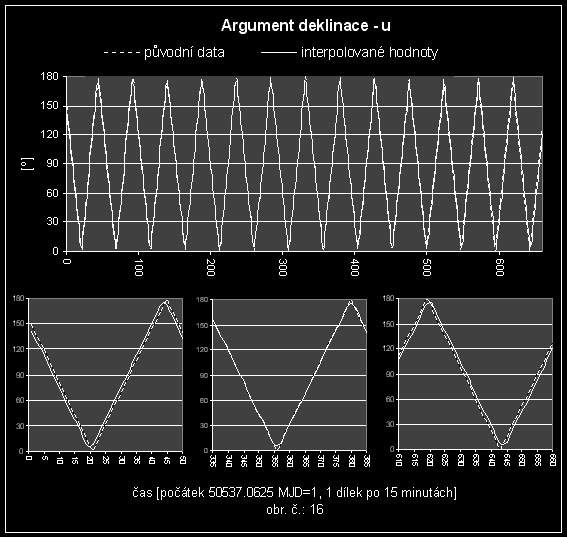
Pro výpočet vyrovnaných koeficientů interpolačních funkcí jsem použil statistický soubor dat z celého týdne, tedy všech 660 časových okamžiků (proč ne 672 je vysvětleno v kapitole [1.6]). Interpolované hodnoty spočtené na základě takto vyrovnaných koeficientů interpolačních funkcí mají tu vlastnost, že se na okrajích takového statistického souboru velmi odchylují od jejich původních hodnot. Naproti tomu s původními hodnotami velmi dobře korespondují uprostřed tohoto statistického souboru (viz. obr. č.: 16). To znamená, že pro výpočet koeficientů interpolačních funkcí není vhodné použít všechna data z celého GPS týdne najednou.
Mnohem přesnějších výsledků bychom pravděpodobně dosáhli použitím menšího statistického souboru dat, tzv. výběrového statistického souboru dat, který by zahrnoval kratší časové období. Tento výběrový soubor dat by obsahoval lichý počet členů (určení jejich počtu by záviselo na dalších výpočtech) a koeficienty interpolačních funkcí spočtené na základě takového souboru bychom přiřadili k prostřednímu bodu tohoto výběrového souboru. Výpočet bychom například provedli postupně pro všechna data jednoho GPS týdne a získali bychom tabelované hodnoty koeficientů interpolačních funkcí pro každý časový okamžik daného GPS týdne. Úloha by tedy přešla na interpolaci v koeficientech interpolačních funkcí. V těchto koeficientech by bylo patrně snazší interpolovat a následně je pak extrapolovat v čase a na základě extrapolovaných koeficientů bychom stanovili mnohem přesnější extrapolované terestrické souřadnice, respektive Keplerovy dráhové elementy.
Ještě lepších výsledků bychom patrně dosáhli použitím metody kolokace nejmenších čtverců. Jedná se o metodu, kdy hledáme korelační vztahy mezi jednotlivými hodnotami statistického souboru a na jejich základě pak stanovíme jistou váhovou matici, kterou zapojíme do výpočtů vyrovnání. Protože se tato metoda zabývá pouze signálem, bylo by nejprve nutné odfiltrovat pozadí časových závislostí, tj. trendy. Potom by tato metoda měla dávat ještě lepší výsledky než postup, který jsem naznačil v předchozím odstavci.
[1] Kosmická geodézie a kosmická geodynamika[5.1] Příloha č.: 1 – Argumenty pro řešení nutace
ARG1
0., 0., 0., 0., 1., -171996., -174.2, 92025., 8.9,
0., 0., 0., 0., 2., 2062. , .2 , -895. , .5 ,
-2., 0., 2., 0., 1., 46. , .0 , -24. , .0 ,
0., 0., 2.,-2., 2., -13187. ,-1.6 , 5736. ,-3.1,
0., 1., 0., 0., 0., 1426. ,-3.4 , 54. ,-0.1,
0., 1., 2.,-2., 2., -517. , 1.2 , 224. ,-0.6,
0.,-1., 2.,-2., 2., 217. ,-0.5 , -95. , 0.3,
0., 0., 2.,-2., 1., 129. , 0.1 , -70. , 0.0,
2., 0., 0.,-2., 0., 48. , 0.0 , 1. , 0.0,
0., 2., 0., 0., 0., 17. ,-0.1 , 0. , 0.0,
0., 2., 2.,-2., 2., -16. , 0.1 , 7. , 0.0,
0., 0., 2., 0., 2., -2274. ,-0.2 , 977. ,-0.5,
1., 0., 0., 0., 0., 712. , 0.1 , -7. , 0.0,
0., 0., 2., 0., 1., -386. ,-0.4 , 200. , 0.0,
1., 0., 2., 0., 2., -301. , 0.0 , 129. ,-0.1,
1., 0., 0.,-2., 0., -158. , 0.0 , -1. , 0.0,
-1., 0., 2., 0., 2., 123. , 0.0 , -53. , 0.0,
0., 0., 0., 2., 0., 63. , 0.0 , -2. , 0.0,
1., 0., 0., 0., 1., 63. , 0.1 , -33. , 0.0,
-1., 0., 0., 0., 1., -58. ,-0.1 , 32. , 0.0,
-1., 0., 2., 2., 2., -59. , 0.0 , 26. , 0.0,
1., 0., 2., 0., 1., -51. , 0.0 , 27. , 0.0
ARG2
2., 0.,-2., 0., 0., 11. , 0. ,
-2., 0., 2., 0., 2., -3. , 1. ,
1.,-1., 0.,-1., 0., -3. , 0. ,
0.,-2., 2.,-2., 1., -2. , 1. ,
2., 0.,-2., 0., 1., 1. , 0. ,
0., 0., 2.,-2., 0., -22. , 0. ,
0., 1., 0., 0., 1., -15. , 9. ,
0.,-1., 0., 0., 1., -12. , 6. ,
-2., 0., 0., 2., 1., -6. , 3. ,
0.,-1., 2.,-2., 1., -5. , 3. ,
2., 0., 0.,-2., 1., 4. , -2. ,
0., 1., 2.,-2., 1., 4. , -2. ,
1., 0., 0.,-1., 0., -4. , 0. ,
2., 1., 0.,-2., 0., 1. , 0. ,
0., 0.,-2., 2., 1., 1. , 0. ,
0., 1.,-2., 2., 0., -1. , 0. ,
0., 1., 0., 0., 2., 1. , 0. ,
-1., 0., 0., 1., 1., 1. , 0. ,
0., 1., 2.,-2., 0., -1. , 0. ,
0., 0., 2., 2., 2., -38. , 16. ,
2., 0., 0., 0., 0., 29. , -1. ,
1., 0., 2.,-2., 2., 29. , -12. ,
2., 0., 2., 0., 2., -31. , 13. ,
0., 0., 2., 0., 0., 26. , -1. ,
-1., 0., 2., 0., 1., 21. , -10. ,
-1., 0., 0., 2., 1., 16. , -8. ,
1., 0., 0.,-2., 1., -13. , 7. ,
-1., 0., 2., 2., 1., -10. , 5. ,
1., 1., 0.,-2., 0., -7. , 0. ,
0., 1., 2., 0., 2., 7. , -3. ,
0.,-1., 2., 0., 2., -7. , 3. ,
1., 0., 2., 2., 2., -8. , 3. ,
1., 0., 0., 2., 0., 6. , 0. ,
2., 0., 2.,-2., 2., 6. , -3. ,
0., 0., 0., 2., 1., -6. , 3. ,
0., 0., 2., 2., 1., -7. , 3. ,
1., 0., 2.,-2., 1., 6. , -3. ,
0., 0., 0.,-2., 1., -5. , 3. ,
1.,-1., 0., 0., 0., 5. , 0. ,
2., 0., 2., 0., 1., -5. , 3. ,
0., 1., 0.,-2., 0., -4. , 0. ,
1., 0.,-2., 0., 0., 4. , 0. ,
0., 0., 0., 1., 0., -4. , 0. ,
1., 1., 0., 0., 0., -3. , 0. ,
1., 0., 2., 0., 0., 3. , 0. ,
1.,-1., 2., 0., 2., -3. , 1. ,
-1.,-1., 2., 2., 2., -3. , 1. ,
-2., 0., 0., 0., 1., -2. , 1. ,
3., 0., 2., 0., 2., -3. , 1. ,
0.,-1., 2., 2., 2., -3. , 1. ,
1., 1., 2., 0., 2., 2. , -1. ,
-1., 0., 2.,-2., 1., -2. , 1. ,
2., 0., 0., 0., 1., 2. , -1. ,
1., 0., 0., 0., 2., -2. , 1. ,
3., 0., 0., 0., 0., 2. , 0. ,
0., 0., 2., 1., 2., 2. , -1. ,
-1., 0., 0., 0., 2., 1. , -1. ,
1., 0., 0.,-4., 0., -1. , 0. ,
-2., 0., 2., 2., 2., 1. , -1. ,
-1., 0., 2., 4., 2., -2. , 1. ,
2., 0., 0.,-4., 0., -1. , 0. ,
1., 1., 2.,-2., 2., 1. , -1. ,
1., 0., 2., 2., 1., -1. , 1. ,
-2., 0., 2., 4., 2., -1. , 1. ,
-1., 0., 4., 0., 2., 1. , 0. ,
1.,-1., 0.,-2., 0., 1. , 0. ,
2., 0., 2.,-2., 1., 1. , -1. ,
2., 0., 2., 2., 2., -1. , 0. ,
1., 0., 0., 2., 1., -1. , 0. ,
0., 0., 4.,-2., 2., 1. , 0. ,
3., 0., 2.,-2., 2., 1. , 0. ,
1., 0., 2.,-2., 0., -1. , 0. ,
0., 1., 2., 0., 1., 1. , 0. ,
-1.,-1., 0., 2., 1., 1. , 0. ,
0., 0.,-2., 0., 1., -1. , 0. ,
0., 0., 2.,-1., 2., -1. , 0. ,
0., 1., 0., 2., 0., -1. , 0. ,
1., 0.,-2.,-2., 0., -1. , 0. ,
0.,-1., 2., 0., 1., -1. , 0. ,
1., 1., 0.,-2., 1., -1. , 0. ,
1., 0.,-2., 2., 0., -1. , 0. ,
2., 0., 0., 2., 0., 1. , 0. ,
0., 0., 2., 4., 2., -1. , 0. ,
0., 1., 0., 1., 0., 1. , 0.
[5.2] Příloha č.: 2 – Seznam řídících a monitorovacích stanic
hlavní řídící stanice:
Colorado Springs (USA)
pozemní řídící stanice:
Ascension Island (jižní Atlantik)
Diego Garcia (Čagoské ostrovy, Indický oceán)
Kwajalwin (Marshallovo souostroví, Tichý oceán)
monitorovací stanice:
Hawai (Tichý oceán)
Ascension Island (jižní Atlantik)
Diego Garcia (Čagoské ostrovy, Indický oceán)
Kwajalein (Marshallovo souostroví, Tichý oceán)
Colorado Springs (USA)
[5.3] Příloha č.: 3 – Programy InterKPL a InterXYZ
V této příloze popíši oba programy, které jsem pro výpočetní zajištění této práce napsal. Kapitola je rozdělena do dvou podkapitol. Každá z nich je věnována jednomu ze dvou programů.
Nyní bych chtěl napsat několik řádek obecně o programech jako o jednom celku. Oba jsou psány v jazyce C++. Jak již bylo výše v práci řečeno, při psaní programů jsem použil interaktivní objektově orientované prostředí C++ Builder 3.0. Oba programy jsou psány jako aplikace pod systémy WIN95, WIN98 a WIN NT. Vstupními formáty souborů jsou soubory SP3 pro vstup terestrických souřadnic družic a ERP pro vstup souřadnic pólu a korekce (UT1-UTC).
Některé výpočetní bloky byly převzaty ze zdrojových textů publikovaných Astronomickým institutem univerzity v Bernu (Astronomical institute, University of Bern). Nicméně jsem tyto bloky musel převést z jazyka FORTRAN do jazyka C++. To obnášelo alespoň základní znalosti syntaxe tohoto programovacího jazyka. Na tyto bloky bude upozorněno dále v textu.
Celkový objem zdrojových kódů obnáší 4726 programových řádek. Jsou to poměrně rozsáhlé programy a proto není možné v této práci jako přílohu uvést jejich vytištěné zdrojové texty. Tyto texty budou na přiloženém CD, které bude obsahovat i ostatní části této diplomní práce v digitální podobě. Obsah přiloženého CD je uveden v příloze č.:4. Stejně tak nemá příliš opodstatnění uvést popis jednotlivých funkcí, metod a procedur, protože jich je mnoho a pak také jsem programy psal tak, že je z názvů jednotlivých procedur, metod a funkcí patrné k jakému účelu slouží. V této příloze budou tedy uvedeny jen některé zajímavé funkce a metody, které nezaberou tolik místa. A nyní již k jednotlivým programům.
Tento program řeší výpočet Keplerových dráhových elementů a jejich následnou interpolaci dle vzorců uvedených v kapitole [1.9]. Po spuštění se otevře vlastní okno programu (obr. č.:17). U horního okraje je menu s položkami, jejichž funkci vysvětlím níže. Pod tímto menu je komunikační okno, pomocí něhož pak program při výpočtu signalizuje jeho stav. Pod tímto oknem je další okno, které má název “Asociované soubory:”. Do tohoto okna se vypisují soubory, které byly určeny jako vstupní. Pod tímto oknem jsou tři stavové řádky. První ukazuje stav právě probíhajících výpočtů. Druhý ukazuje číslo družice pro kterou se právě výpočet provádí a dále délku ukončeného výpočtu. Poslední stavová řádka ukazuje aktuální adresář.
Před samotným výpočtem je třeba provést několik nastavení. Za prvé je nutné nastavit číslo družice, pro kterou chci výpočet provést. To se provádí pomocí menu [Program à Nastavení à Číslo družice]. Implicitně je nastavena družice PRN1. Dále se musí zadat soubor se souřadnicemi pólu a korekcí (UT1-UTC). To se provede v menu [Program à Nastavení à Soubor *.erp]. Dále je třeba nastavit, kolik dní bude vzato do výpočtu. Implicitně nastaveno je 7, tedy celý týden. Klávesami F2-F7 nebo přímo v položce [Soubory à Min. počet asoc. souborů] je možné tento údaj měnit. Dalším nutným krokem je tyto soubory asociovat. Je možné tento úkon provést kombinací kláves CTRL+A a nebo v menu [Soubory à Asociovat]. Každý soubor se musí asociovat samostatně. Pokud chceme odstranit nějaký soubor z našeho výběru, můžeme jej odstranit dvojím kliknutím myši na název souboru s cestou v panelu “Asociované soubory:” a nebo v menu [Soubory à Deasociovat]. Posledním úkonem, který před vlastním výpočtem je třeba provést, je nastavení přibližných hodnot amplitud, fázových posunů, period a trendů. To se provádí pomocí menu [Program à Nastavení à Přibližné koeficienty] a nebo dvojím kliknutím myší na prostřední stavový řádek dole. Implicitně jsou zde nastaveny přibližné hodnoty těchto veličin pro družici PRN1 a GPS týden 899. Kliknutím na volnou plochu programu se zadávání ukončí. Nyní můžeme spustit samotný výpočet. Provedeme kontrolu asociovaných souborů pomocí menu [Soubory à Kontrola vstupní konfigurace] nebo kombinací kláves CTRL+K a pak spustíme výpočet v menu [Výpočet à Spustit] nebo kombinací kláves CTRL+V. Výsledný výpočetní protokol lze pak uložit pomocí kláves CTRL+U nebo v menu [Soubory à Záznamy výpočtů à Uložit záznam výpočtů]. Ještě je dobré říci, že program je vybaven nápovědou v podobě tzv. HINTů, tj. pokud kurzor myši zůstane na části programu déle, objeví se vedle něj okénko s průvodním textem. A poslední poznámka k tomuto programu je, že je výhodné v menu [Soubory à Změna adresáře] nebo klávesami CTRL+Z nastavit adresář vstupních souborů
*.sp3.Nyní bych rád uvedl příklad převzatého výpočetního bloku, který jsem přepsal z jazyka FORTRAN do jazyka C++. Jedná se výpočet nutační matice. Tedy původní zdrojový text v jazyce FORTRAN má tento formát:
C*Za řádkem "C DATA" následuje seznam argumentů pro výpočet lineární kombinace Delauneyových proměnných. Tento seznam jsem z ukázky odebral, neboť osahuje jen samá čísla a byl několik stánek dlouhý. Seznam těchto argumentů je uveden v příloze č.:1.
A mnou napsaný zdrojový text, který řeší stejnou problematiku, tedy počítá nutační matici, je následující:
Mat<>MaticeNutace(double TGPS)Program InterXYZ řeší po výpočetní stránce problematiku interpolace v terestrických souřadnicích družic. Jeho ovládání je podobné jako u programu InterKPL, ale je jednodušší. Po spuštění se objeví opět samostatné okno tohoto programu. Toto okno je až na název totožné s oknem programu InterKPL.
Asociace, změna adresáře, ukládání protokolů, deasociace souborů a nastavení počtu dnů vzatých do výpočtů je naprosto stejné jako u programu InterKPL. Změnilo se jen zadávání přibližných koeficientů a nastavení PRN počítané družice. Dále odpadlo nastavení souboru se souřadnicemi pólu a korekcí (UT1-UTC).
Při výpočtech postupujeme stejně jako v kapitole [5.3.1] až na malé rozdíly, které jsou: zadání přibližných koeficientů interpolačních funkcí (viz. kapitola [1.8]) je zde v menu [Soubory à Přibližné koeficienty], nebo je možné vyvolat pomocí klávesové zkratky CTRL+P. Podobně jako u programu IterKPL, jsou i zde přednastaveny přibližné hodnoty těchto koeficientů pro družici PRN1 a GPS týden 899. Zadání čísla družice je v menu [Soubory à Číslo družice], nebo pomocí klávesové zkratky CTRL+C.
[5.4] Příloha č.: 4 – Obsah přiloženého CD
Adresář:obsahuje data pro GPS týdny 899 a 900. Tj. terestrické souřadnice družic a souřadnice pólu a korekce (UT1-UTC) a to jak finální tak i predikované.
obsahuje spustitelné programy InterKPL a InterXYZ, zajišťující po výpočetní stránce problematiku této diplomové práce.
obsahuje různé doprovodné soubory ve formátech EXCEL 97 a TXT, vzniklé během zpracovávání tématu. Tyto soubory jsou bez jakýchkoliv grafických úprav a obsahují hrubé dokumenty.
obsahuje text diplomové práce ve formátu WORD 97 a RTF.
obsahuje všechny zdrojové texty programů, které jsem programoval v jazyce C++, zdrojové texty některých výpočetních bloků v jazyce FORTRAN a konečně zdrojové texty hlavičkových souborů gmatvec pro práci s maticemi, které napsal doc. Ing. Aleš Čepek, CSc z katedry Mapování a kartografie a které mi poskytl.
Viz. hlavni dokument DP. Děkuji za pochopení.