Klasifikace :
Kuželové konformní zobrazení.

Popis zeměpisné sítě :
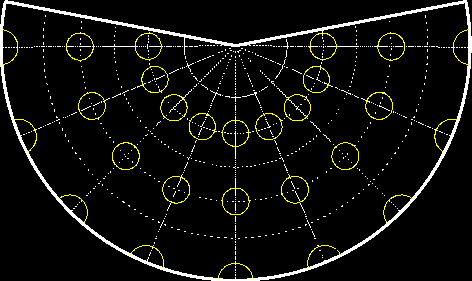
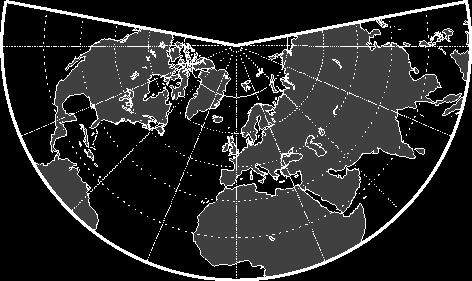
Poledníky se zobrazí jako přímky, které se protínají v jednom bodě a to v kartografickém pólu zobrazení. Pokud se jedná o zobrazení v normální poloze, pak je kartografický pól totožný s pólem zeměpisným. Rovnoběžky se zobrazí jako koncentrické části kružnic, jejichž střed je v kartografickém pólu zobrazení. Vzdálenost obrazů rovnoběžek se se vzdáleností od kartografického pólu (v případě normální polohy zobrazení pak od pólu zeměpisného) zvětšují. Pokud se jedná o zobrazení v normální poloze, pak se pól, který je bližší základní rovnoběžce, zobrazí jako bod a opačný pól se nezobrazí. Zobrazení je symetrické podle každého poledníku.

Průběh zkreslení :
Délkově se nezkreslují obě základní rovnoběžky. Délkové zkreslení je konstantní podél rovnoběžek a v daném bodě pak i v každém směru (podmínka konformity).

Zobrazovací rovnice :
n = ln(cosf₁/cosf₂)/ln[tan(p/4 + f₂/2)/tan(p/4 + f₁/2)]
F = cosf₁.tanⁿ(p/4 + f₁/2)/n
r = R.F/tanⁿ(p/4 + f/2)
q = n(l - l₀)
x = r.sinq
y = r₀ - r.cosq

kde r₀ vypočteme tak, že za f dosadíme f₀. Pokud bychom chtěli jen jednu nezkreslenou rovnoběžku nebo v případě že by se f₁ = f₂, bude platit relace: n = sinf₁.

Náhledy :