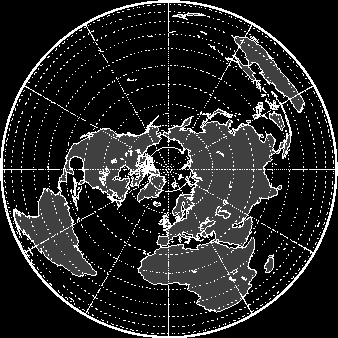
Klasifikace :
Azimutální ekvivalentní neperspektivní zobrazení v normální, příčné a obecné poloze.

Popis zeměpisné sítě :
normální poloha -
Poledníky se zobrazí jako přímky vycházející z pólu. Úhle mezi nimi je stále konstantní. Rovnoběžky se zobrazí jako kružnice, jejichž střed tvoří pól (kartografický i zeměpisný). Vzdálenosti obrazů rovnoběžek se se vzdáleností od pólu zmenšují. Rovník a druhá polokoule mohou být zobrazeny. Jeden pól se zobrazuje jako bod, druhý pól se zobrazí jako kružnice o 1,41 krát větším poloměru než rovník. Zobrazení je symetrické podle každého poledníku.

příčná poloha -
Základní poledník se zobrazí jako přímka. Poledník +-90^o od základního poledníku se zobrazí jako kružnice. Ostatní poledníky jsou komplexní křivky, které se protínají na pólech. Vzdálenosti obrazů poledníků se se vzdáleností od základního poledníku zmenšují. Póly se zobrazují jako body. Rovník se zobazí jako přímka. Ostatní rovnoběžky se zobrazí jako komplexní křivky, které jsou konkávní vzhledem k nejbližšímu pólu a nemají na základním poledníku konstantní rozestup. Ten se se vzdáleností od rovníku zmenšuje. Na poledníku +-90^o od základního poledníku mají rovnoběžky konstantní rozestup. Zobrazení je symetrické podle základního poledníku a rovníku.

obecná poloha -
Základní poledník se zobrazí jako přímka. Ostatní poledníky jsou komplexní křivky, které se protínají ve zobrazeném pólu. Pól se zobrazí jako bod. Rovnoběžky jsou komplexní křivky, které nemají podél základního poledníku konstantní rozestup. Ten se zmenšuje se vzdáleností od kartografického pólu zobrazení. Zobrazení je symetrické podle základního poledníku.

Průběh zkreslení :
Podél kartografických rovnoběžek je zkreslení konstantní. Zkreslení roste se vzdáleností od kartografikého pólu. Jediným nezkresleným bodem je kartografický pól. Maximálních hodnot zkreslení dosahuje zobrazení okolo okraje zobrazení. Extrémních hodnot dosahuje zkreslení při zobrazení celé Země.

Zobrazovací rovnice :
normální poloha -
          r = 2.R.(p/4 - f/2)
          x = r.sin(l - l₀)
          y = -r.cos(l - l₀)

příčná poloha -
          cos z = cosf cos(l - l₀)
          K = [2/(1 + cos z)]^1/2
          x = R.K.cosf sin(l - l₀)
          y = R.K.sinf

obecná poloha -
          cos z = sinf₁ sinf + cosf₁ cosf cos(l - l₀)
          K = [2/(1 + cos z)]^1/2
          x = R.K.cosf sin(l - l₀)
          y = R.K.[cosf₁ sinf - sinf₁ cosf cos(l - l₀)]

Náhledy :