Klasifikace :
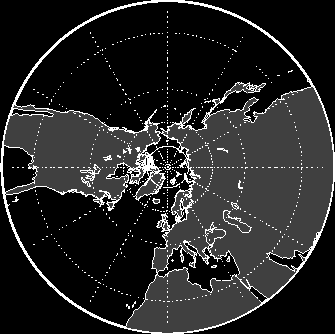
Azimutální zobrazení v normální, příčné a obecné poloze (perspektiva). Není ani konformní ani ekvivalentní.

Popis zeměpisné sítě :
normální poloha -
Poledníky se zobrazí jako přímky vycházející z pólu. Úhle mezi nimi je stále konstantní. Rovnoběžky se zobrazí jako kružnice, jejichž střed tvoří pól (kartografický i zeměpisný). Vzdálenosti obrazů rovnoběžek se se vzdáleností od pólu zvětšují. Rovník ani protější polokoule nejsou zobrazeny. Pól se zobrazuje jako bod. Zobrazení je symetrické podle každého poledníku.

příčná poloha -
Poledníky se zobrazují jako rovnoběžné přímky, jejichž rozestupy se se vzdáleností od základního poleníku zvětšují. Nezobrazí se poledníky, které nejsou v intervalu od +90^o do -90^o od základního poledníku. Rovník se zobrazí jako přímka. Rovnoběžky se zobrazí jako hyperboly konvexní vzhledem k rovníku. Vzdálenost obrazů rovnoběžek se směrem k pólům zvětšuje. Póly se nezobrazí. Zobrazení je symetrické podle rovníku a podle základního poledníku.

obecná poloha -
Poledníky se zobrazí jako přímky vycházející ze zeměpisného pólu. Rovník se zobrazí jako přímka kolmá na základní poledník. Jestliže je kartografický pól (leží na základním poledníku) na severní polokouli a jeho zeměpisná šířka je f₀, pak rovnoběžka o zeměpisné šířce (90^o - f₀) se zobrazí jako parabola. Severnější rovnoběžky se zobrazí jako elipsy a jižnější jako hyperboly. Všechny konkávní k nejbližšímu pólu. Pokud je kartografický pól na jižní polokouli, pak je to právě naopak. Zobrazení je symetrické podle základního poledníku. Pól se zobrazuje jako bod.

Průběh zkreslení :
Ke zkreslení délek, ploch a úhlů nedochází pouze v kartografickém pólu. Všude jinde dochází ke zkreslení délek, ploch i úhlů. Zkreslení se rychle zvětšuje směrem od kartografického pólu. Zkreslení je konstantní na kartografických rovnoběžkách.

Zobrazovací rovnice :
normální poloha -
          r = R.cotgf
          x = r.sin(l - l₀)
          y = -r.cos(l - l₀)

příčná poloha -
          x = R.tan(l - l₀)
          y = R.tanf/cos(l - l₀)

obecná poloha -
          cos z = sinf₁ sinf + cosf₁ cosf cos(l - l₀)
          K = sec z
          x = R.K.cosf sin(l - l₀)
          y = R.K.[cosf₁ sinf - sinf₁ cosf cos(l - l₀)]

Náhledy :