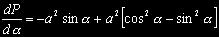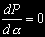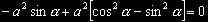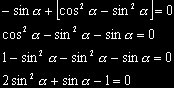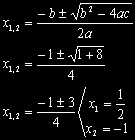Výpočet maximálního objemu plechového žlabu
Zpět ||
Zpět na hlavní stránku
Zadání:
Plechová žlab má průřez rovnoramenného lichoběžníku. Menší základna a obě ramena mají stejnou
délku 30cm. Jak široký musí být žlab nahoře, aby pojal co nejvíce vody?
Řešení:
 a = 30 cm
a = 30 cm
P = ? ; P = Pmax
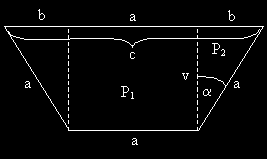
Musíme sestavit rovnici pro plochu takového obrazce. Ta je složena z částečných ploch tak,
jak je naznačeno v náčrtu.
P = P1 + 2.P2
P1 = a . v = a . a . cos a = a2 . cos a
P2 = (1/2) . v .b = (1/2) . a . cos a . a . sin a = (1/2) . a2 . cos a . sin a
P = a2 . cos a + 2 . (1/2) . a2 . cos a . sin a
P = a2 . cos a + a2 . cos a . sin a
Protože hledáme maximum plochy (hledáme extrémy), budeme tuto plochu derivovat a danou
derivaci položíme rovnu nule. A protože se nám horní šířka a výška žlabu mění s úhlem a,
budeme rovnici plochy derivovat podle proměnné a.
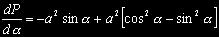
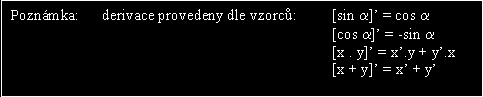
A protože hledáme maximum, položíme derivaci rovnu nule: 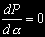
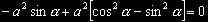
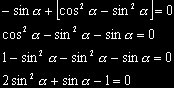

Následuje substituce sin a = x:
2 . x2 + x – 1 = 0
A řešení kvadratické rovnice dle známého vzorce:
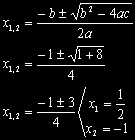
A ze substituce vyplývá:
a1 = 30°
a2 = 270°
Případ a2 je případ, kdy bychom hledali plochu minimální,
tedy nulovou a případ a1 je případ, kdy hledáme plochu
maximální. Tedy přesně to, co my potřebujeme.
Z obrázku je patrné, že:
b = a . sin a = 15 cm
A tedy, horní šíře žlabu c bude rovna:
c = 2 . b + a = 60 cm
|| Seznam || AltaVista || Yahoo ||