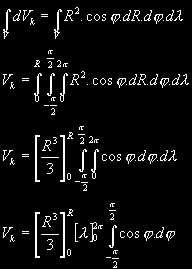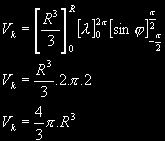Objem koule
Zpět ||
Zpět na hlavní stránku
Na základní škole najednou tenhle vzoreček spadne z nebe a musíte se ho naučit. Problém ale je,
že je to něco, co pro vás v tu chvíli musí platit, protože to paní učitelka řekla, ale rozhodně se
neví - a leckdy ani nechce vědět - proč to tak je a kde se tenhle vzoreček vzal. Na střední škole
se s tímto vzorečkem počítá stále častěji, ale opět, kde se vzal tu se vzal... Nikdo Vám ho neodvodí.
A v té době se zvídavější žáci začínají ptát, proč zrovka takhle ten vzorec platí. Proč ne jinak.
Řešení je nakonec docela jednoduché. Protože je to spojité těleso budeme to počítat integrálem.
Ale co vlastně budeme integrovat? Přímo rovnici této plochy by bylo dost složité a bylo
by to počítánína docela dlouho… Cesta tedy tudy vede, ale je dlouhá a namáhavá. A člověk je od
přírody pohodlný a tak hledal jednodušší, ale korektní, cestu jak vyřešit a dopočítat se tohoto
vztahu. A kouzlo se povedlo.
Vezmeme diferenciálně (nekonečně) malinkatý kousek objemu koule a pak tyhle kousky
integrálem sečteme. V mluvě matematických formulí to vypadá takto:
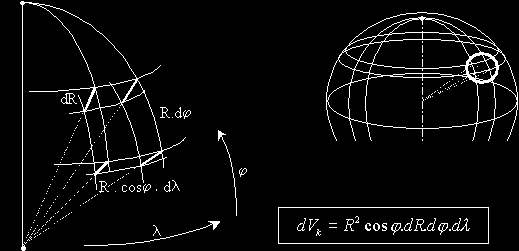
Hodnota dVk je diferenciálním (nekonečně malým) objemkem části koule. Ve
všech souřadnicích, které jsme na kouli zavedli (říká se jim sférické) se pohybujeme v diferenciálních
hodnotách a tak diferenciální objemek můžeme spočítat jako kvádřík a nebrat v potaz, že je to ve
zkutečnosti nekonečne malá kulová slupička.
A nyní je čas na integraci. Jedná se o objemový integrál (trojný) přes všechny diferenciály:
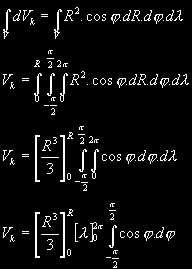
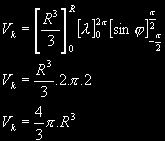
A hle, vzoreček pro výpočet objemu koule je na světě :-))) Tento příklad je jednoduchý, ale pro
názornost bohatě postačí.
Problém se začíná zahušťovat ve chvíli, kdy se jedná například o rotační
elipsoid (necháte elipsu rotovat podél své vedlejší poloosy). Tam se totiž veličina u koule zvaná
poloměr R nedá použít, neboť ten se u elipsoidu spojitě mění. Zavádí se do výpočtů meridiánový
a příčný poloměr M a N. To jsou funkce obecně souřadnice j
a figuruje tam i číselná excentricita a poloosy elipsoidu jakožto jeho konstanty.
Další zahuštění výpočtů přijde s trojosým elipsoidem. Atd...
|| Seznam || AltaVista || Yahoo ||