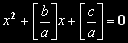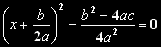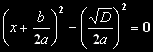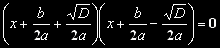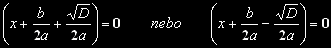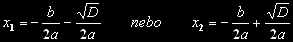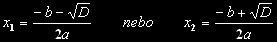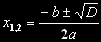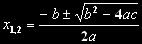Řešení kvadratické rovnice
Zpět ||
Zpět na hlavní stránku
Na základní škole, ale většinou až na střední škole se učí studenti počítat
kvadratické rovnice. Někteří učitelé vzoer pro výpočet kořenů (řešení)
takových rovnic napíší na tabuli bez odvození a jiní je odvozují. Já patřím do té
druhé skupiny. Z toho důvodu (a i z jiných) toto odvození publikuji na svých stránkách
hlavně pro studenty ale i pro učitele. Takže pusťme se do toho!
Obecný tvar kvadratické rovnice (pozor, ne obecné rovnice druhého stupně!!!) je tento:
a.x2 + b.x + c = 0
Abychom mohli dále počítat, je třeba takovouto rovnici upravit na tvar, kdy je
koeficient u členu x2 roven jedné:
a.x2 + b.x + c = 0 / :a
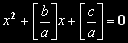
Teď na chvíli odhlédneme od absolutního členu [c/a] a budeme se
věnovat jen členům, které obsahujíé proměnnou x. Musíme si vzpomenout
na tento vzorec:
(A + B)2 = A2 + 2AB + B2
A podle tohoto vzorce doplníme členy obsahující proměnnou x na čtverec.
Je zřejmé, že:
A2 = x2 => A = x
2AB = [b/a]x
Po dosazení za A dostáváme:
2xB = [b/a]x => B = [b/2a]
A teď nám nic nebrání tomu, abychom tyto hodnoty dosadili do výrazu definujícího
kvadratickou rovnici (tj. přičteme a odečteme výraz odpovídající hodnotě B):

První tři členy tohoto výrazu tvoří výše zmíněný vzorec a polední dva
členy pak pouze sečteme:
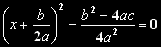
Zavedeme nyní pojem diskriminantu a označíme jej písmenem D. Bude se rovnat:
D = b2 - 4ac
Pak můžeme předešlý výraz kvadratické rovnice přepsat do tohoto tvaru:
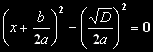
Opět si vzpomeneme na jeden z algebraických vzorců. Konkrétně na tento:
A2 - B2 = (A + B)(A - B)
A podle něj rozložíme rovnici na tento tvar:
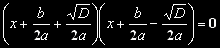
A teď nastupuje úvaha, kdy se levá strana takovéto rovnice rovná nule.
To nastane, když se jedna závorka v součinu rovná nule, nebo když se druhá
závorka v součinu rovná nule a nebo když se v součinu obě závorky na levé straně
rovnice rovnají nule. Takže:
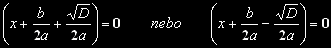
Z toho vyplývá, že (jednotlivá řešení označíme jako x1 a x2):
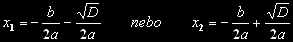
A dále na základě jednoduchých úprav:
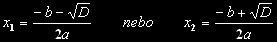
Tato dvě řešení sloučíme do jednoho a vzorce nám přejdou na tvar:
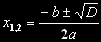
Poslední úpravou je, že za symbol diskriminantu D dosadíme opět
výraz b2 - 4ac a tím je odvození pro vztahu pro výpočet
kořenů kvadratické rovnice hotov:
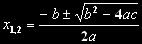
|| Seznam || AltaVista || Yahoo ||