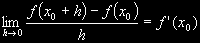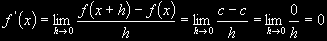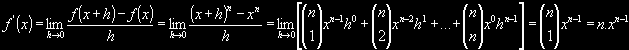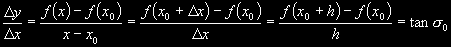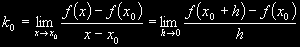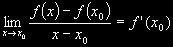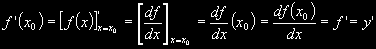Derivace
Zpět ||
Zpět na hlavní stránku
Na střední škole se studenti dostávají k pojmu derivací. Na tabuli jim sice učitelé vysvětlí, že
derivace je vlastně limita jistého podílu, kterému se říká diferenční, že když se to
nakreslí tak to vypadá takhle a takhle... Napíší tak tu limitu jako definici derivace a pak
do studentů začnou hustit vzorce pro derivování... Případně ještě odkáží na tabulky... A to je vše...
A při tom všem vůbec neuvažují o tom, ukázat studentům jak vlastně tyhle vzorce pro
derivování vznikly... Že nespadli z nebe, že je někdo odvodil. A nakonec ani nedoufají v to, že
by studenti postup odvození alespoň základních derivací mohli pochopit. A přitom to není
až tak těžké a nepochybuji o tom, že kdo ze studentů se nad tím trochu zamyslí, nebude
pro něj problém si pak některé vzorce místo biflování zpaměti přímo z definice derivace odvodit.
A proto, HURÁ na to!!!
Takže nejdříve trochu teorie... Hodně často při vyšetřování průběhu funkcí nás zajímá,
jak rychle dochází ke změně funkčních hodnot dané funkce vůči velikosti přírůstku argumentu.
Nebo-li, jak je velká či malá změna funkční hodnoty vůči změně argumentu. A právě tuhle
vlastnost zkoumáme pomocí zlomku, kterému se říká diferenční (už jsem o něm psal výše)
a má tento tvar:
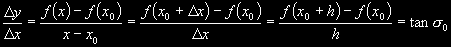
Když si to nakreslíme, vypadá situace následovně:
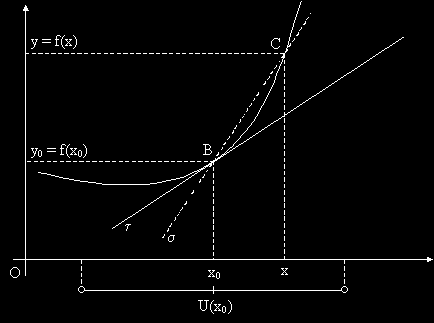
Je zcela zřejmé, že diferenční zlomek nám vyjadřuje směrnici sečny s.
Nás ale bude zajímat případ, kdy se naše x limitně blíží x0. Budeme tedy hledat
smernici přímky (tečny t), která má rovnici (vycházející
z obecné rovnice přímky):
y – y0 = k0.(x – x0)
nebo - li
f(x) – f(x0) = k0.(x – x0)
Zvolíme tedy bod C = [x, f(x)] takový, že x Î U(x0) a x ą x0.
Body B a C vytvoří již zmiňovanou sečnu.
Lze tedy očekávat, že při x ® x0 se bude C ® B
a sečna s ® tečně t. Řekneme potom, že přímka t je tečnou
grafu funkce f(x) v bodě x0 právě tehdy, když platí:
1) tečna t prochází bodem
B = [x0, f(x0)]
2) tečna t má směrnici:
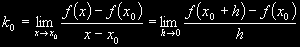
Definice vlastní/nevlastní derivace
Na základě výše zmíněných vlastností tečny definujeme tedy derivaci takto: říkáme, že
funkce f(x) definovaná na jistém U(x0) má vlastní/nevlastní derivaci prvního řádu v
bodě x0, právě když existuje vlastní/nevlastní limita:
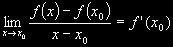
Analogickým způsobem definujeme i vlastní/nevlastní derivace zprava a zleva. V různých
matematických učebnicích a textech se zkutečnost, že funkce f(x) má derivaci zapisuje různě.
Nejpoužívanějšími zápisy jsou tyto:
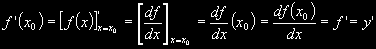
Funkce f(x) má v bodě x0 první derivaci f’(x0) právě když má
v bodě x0 derivaci z leva f-’(x0) i derivaci
zprava f+’(x0), přičemž se tyto derivace rovnají.
Definice derivace funkce na intervalu:
Funkce f(x) má 1. derivaci f’(x) na otevřeném intervalu (a, b) právě, když pro
každé x Î (a, b) existuje derivace f’(x).
Funkce f(x) má derivaci f’(x) na uzavřeném intervalu právě, když
existují derivace f’(x) na intervalu (a, b) a existují i derivace f+’(a) a f-’(b).
Funkce f(x) má derivaci f’(x) na polouzavřeném intervalu +’(a).
Funkce f(x) má derivaci f’(x) na polouzavřeném intervalu (a, b> právě, když existují
derivace f’(x) na intervalu (a, b) a existuje i derivace f-’(b).
Odvození derivačních vzorců:
Tak pro tuto chvíli teorii bylo učiněno zadost a teď se vrhneme na odvození
některých jednodušších derivačních vzorečků. Všechny vzorce budeme odvozovat
z definice derivace, takže pro připomenutí, derivace je definována limitou:
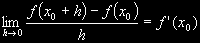
A teď už konečně samotná odvození:
f(x) = c = konstanta
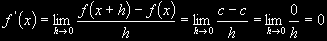
f(x) = xn
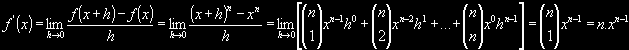
f(x) = sin x

f(x) = ex
|| Seznam || AltaVista || Yahoo ||