Trajektorie bodu v analytice (1)
Zpět ||
Zpět na hlavní stránku
Zadání:
Napiště rovnici křivky, po které se pohybuje bod M = [x; y]
ležící dvakrát dále od osy x než od přímky vyjádřené rovnicí p: x = -3.
Řešení:
Nejprve se musíme na příkladem zamyslet. Říkají nám, že máme napsat rovnici křivky,
po které se pohybuje bod M. A máme daný poměr vzdáleností tohoto bodu od osy x a
od dané přímky p.
Vzhledem k tomu, že onen poměr je nějaké číslo (v našem případě číslo 2) a kolmé vzdálenosti
mají být měřeny od přímek (osa x je jistě přímkou, stejně tak jako zadaná
přímka p), bude naše křivka, jejíž rovnici máme napsat, také přímkou. Označme ji q.
Poznámka:
Přímka je křivka s nulovou křivostí K. Křivost K vyjadřuje zlomek K = 1/R, kde
hodnota R je hodnota poloměru křivosti dané křivky. U kružnice je to například
přímo její poloměr. Budeme-li poloměr kružnice dále zvětšovat, bude se nám hodnota
křivosti K zmenšovat (viz. vzorec v druhé větě poznámky). Tak dospějeme do situace,
kdy bude hodnota poloměru křivosti R naší kružnice nekonečně velká R = Ą a proto bude
hodnota křivosti rovna nule: K = 1/R = 1/Ą = 0. Tak nám kružnice degraduje na přímku.
Přímka se obecně definuje jako křivka, která má v každém svém bodě křivost rovnu nule.
Takže už víme, že onou křivkou popisující trajektorii bodu M bude přímka. Teď je
třeba si situaci řádně nakreslit:
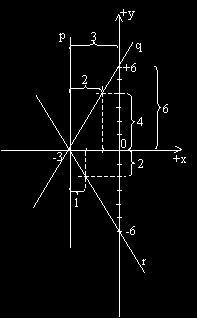
Při kreslení obrázku musíme uvažovat takto. Přímka p má od osy y konstatní
vzdálenost rovnu 3. Bod M přitom musí mít vzdálenost od osy x rovnu dvojnásobku
vzdálenosti od přímky p. Všechny body na ose y mají od přímky p vzdálenost 3.
Takže hledáme nyní bod na ose y takový, jehož vzdálenost od osy x bude rovna
dvojnásbku vzdálenosti od přímkly p, tedy takový, jehož vzdálenost
od osy x bude rovna 6. Takovým bodem je bod o souřadnicích [0; 6].
Tak jsme našli první bod přímky q, která vyjadřuje definovanou trajektorii bodu M.
A teď potřebujeme najít druhý bod přímky q. Podívejme se nyní na průsečík přímky p
s osou x.
Tento bod leží přímo na zadané přímce p a zároveň na ose x. Otázka nyní je, zda platí,
že tento bod je dvakrát dále od osy x než od přímky p. Od přímky p má vzdálenost
rovnu nule. Od osy x má rovněž vzdálenost rovnu nule. A 2*0 = 0, takže i takový bod je
dvakrát dále od osy x než od přímky p. Máme tedy dva body, které leží na naší hledané
přímce q.
V tuto chvíli jsme schopni odvodit rovnici trajektorie bodu M. Oba známé body
označíme P, Q. Sestrojíme dále směrový vektor PQ přímky q:
PQ = sq = Q - P
sq = (XQ - XP; YQ - YP)
sq = (0 - (-3); 6 - 0) = (3; 6)
Známe bod na přímce q (jeden z bodů P a Q) a známe její směrový vektor. Nic nám nebrání
sestavit parametrické vyjádření přímky q:
x = XQ + t*sq1
y = YQ + t*sq2
x = 0 + 3t = 3t
y = 6 + 6t
Z parametrického vyjádření trajektorie odvodíme její obecnou rovnici
vyloučením parametru t. Úpravy budou následující:
x = 0 + 3t = 3t / *(-2)
y = 6 + 6t
-2x = -6t
y = 6 + 6t
Obě rovnice sečteme a dále upravíme:
y + (-2x) = 6 + 6t + (-6t)
y - 2x = 6
y = 2x + 6
y = 2(x + 3)
Výsledek je:
q: y = 2(x + 3)
Toto je směrnicové vyjádření rovnice trajekntorie bodu, který je vždy dvaktrát dále od osy x
než od přímky p. Z obrázku je ale dobře patrné, že takové přímky existují dvě.
My jsme zatím odvodily pouze jednu. A to tu, jejíž graf je rostoucí, tedy přímku q.
Zbývá ještě odvodit rovnici přímky r. Můžeme postupovat úplně stejně i v případě
odvození rovnice přímky r. My se ale trochu zamyslíme a přijdeme na to, že přímka
r je vůči přímce q (jejíž rovnici již máme odvozenou) otočená o 90o.
Takže rovnice zůstane stejná, jen se nám změní znaménko u směrnice:
q: y = 2(x + 3)
r: y = -2(x + 3)
Toto jsou tedy obě přímky, p a r, vyjadřující dráhu uvažovaného bodu M. Výsledek můžeme
zapsat také ve tvaru:
y = ±2(x + 3)
|| Seznam || AltaVista || Yahoo ||
